题目内容
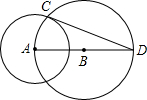如图，⊙B经过⊙A的圆心，且与⊙A交于点C，直线AB交⊙B于点D，求证：CD是⊙A的切线．
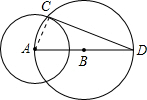证明：连接AC，∵AD是⊙B的直径，
∴∠ACD=90°．
∴AC⊥CD，又AC是⊙A的半径．
∴CD是⊙A切线，C是切点．
分析：要证CD是⊙A的切线，只要连接AC，再证∠ACD=90°即可．
点评：本题考查了切线的判定．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．
练习册系列答案
阅读快车系列答案
相关题目
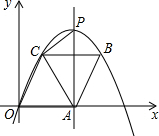、C在这条抛物线上，如果四边形OABC是菱形，
（2013•太原二模）如图，经过原点的抛物线y1=x2+2x与x轴交于点A，将它平移得到抛物线y2=（x-2）2+1．有以下结论：
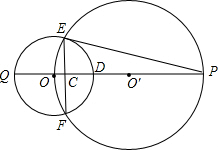于点C，交⊙O于点Q，且EF=2