Question

如图，⊙O′经过⊙O的圆心，E、F是两圆的交点，直线OO′交⊙O′于点P，交EF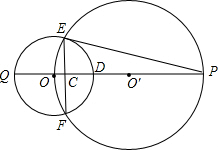于点C，交⊙O于点Q，且EF=2

15

，sin∠P=

1

4

．
（1）求证：PE是⊙O的切线；
（2）求⊙O和⊙O′的半径的长；
（3）若点A在劣弧

QF

上运动（与点Q、F不重合），连接PA交劣弧

DF

于点B，连接BC并延长交⊙O于点G，设CG=x，PA=y，求y关于x的函数关系式，并写出自变量x的取值范围．

Answer 1

分析：（1）要想证PE是⊙O的切线，只要连接OE，求证∠OEP=90°即可．
（2）利用相交弦的性质与三角函数和勾股定理来确定圆的半径．
（3）利用切线长定理、相交弦定理、相似比来确定y与x的函数关系．

解答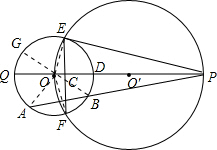：（1）证明：连接OE，
∵OP是⊙O'的直径，
∴∠OEP=90°．
∴PE是⊙O的切线．

（2）解：设⊙O、⊙O'的半径分别为r，r'
∵⊙O与⊙O'交于E、F，
∴EF⊥OO'，EC=

1

2

EF=

15

．
∴在Rt△EOC、Rt△POE中，∠OEC=∠OPE．
∴sin∠OEC=sin∠OPE=

1

4

．
∴sin∠OEC=

OC

OE

=

OC

r

=

1

4

．
即OC=

1

4

r，
∴r2-

1

16

r2=15，解得r=4．
Rt△OPE中，sin∠OPE=

OE

OP

=

r

2r′

∴r'=8．

（3）解：连接OF，
∵∠OEP=90°，CE⊥OP，
∴PE²=PC•PO．
又∵PE是⊙O的切线，
∴PE²=PB•PA．
∴PC•PO=PB•PA．
即

PC

PA

=

PB

PO

，
又∵∠CPB=∠APO，
∴△CPB∽△APO．
∴

BC

OA

=

PC

PA

．
∴BC=

60

PA

．
由相交弦定理，得BC•CG=CF•CE．
∴BC=

15

CG

．
∴PA=4CG．
即y=4x（

15

＜x＜5）．

点评：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．