题目内容
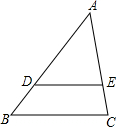已知：如图，△ABC中，DE∥BC，| AD |
| AB |
| 2 |
| 3 |
| A、2：3 | B、2：5 |
| C、4：9 | D、4：25 |
分析：由于DE∥BC，那么△ADE与△ABC相似；已知了AD、AB的比例关系，即两相似三角形的相似比．根据相似三角形的面积比等于相似比的平方，即可得出所求的结论．
解答：解：∵DE∥BC
∴△ADE∽△ABC
∵
=
∴
=(
)2=(
)2=
．
故本题选C．
∴△ADE∽△ABC
∵
| AD |
| AB |
| 2 |
| 3 |
∴
| SADE |
| SABC |
| AD |
| AB |
| 2 |
| 3 |
| 4 |
| 9 |
故本题选C．
点评：此题考查了相似三角形的性质，相似三角形的面积比等于相似比的平方；还考查了相似三角形的判定，平行于三角形一边的直线与三角形另两边或另两边的延长线所组成的三角形与原三角形相似．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17、已知，如图，△ABC中，∠BAC=90°，AD⊥BC于点D，BE平分∠ABC，交AD于点M，AN平分∠DAC，交BC于点N．
已知：如图，∠ABC、∠ACB 的平分线相交于点F，过F作DE∥BC于D，交AC 于E，且AB=6，AC=5，求三角形ADE的周长．
已知：如图，△ABC是等边三角形，点D在AB上，点E在AC的延长线上，且BD=CE，DE交BC于F，求证：BF=CF+CE．
已知：如图，△ABC中，AB=AC=10，BC=16，点D在BC上，DA⊥CA于A．
已知：如图，△ABC中，AD⊥BC，BD=DE，点E在AC的垂直平分线上．