题目内容
 如图,直线AB交CD于点O,由点O引射线OG、OE、OF,使OC平分∠EOG,∠AOG=∠FOE,∠BOD=56°,求∠FOB的度数.
如图,直线AB交CD于点O,由点O引射线OG、OE、OF,使OC平分∠EOG,∠AOG=∠FOE,∠BOD=56°,求∠FOB的度数.考点:对顶角、邻补角,角平分线的定义
专题:
分析:根据对顶角相等可得∠AOC=∠BOD,再求出∠AOC=∠COF,然后根据平角等于180°列式计算即可得解.
解答:解:由对顶角相等可得,∠AOC=∠BOD=56°,
∵OC平分∠EOG,
∴∠1=∠2,
∵∠AOG=∠FOE,
∴∠1+∠FOE=∠2+∠AOG,
即∠AOC=∠COF=56°,
∴∠FOB=180°-∠AOC-∠COF=180°-56°-56°=68°.
∵OC平分∠EOG,
∴∠1=∠2,
∵∠AOG=∠FOE,
∴∠1+∠FOE=∠2+∠AOG,
即∠AOC=∠COF=56°,
∴∠FOB=180°-∠AOC-∠COF=180°-56°-56°=68°.
点评:本题考查了对顶角相等,邻补角的定义,角平分线的定义,熟记概念并求出∠AOC=∠COF是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )
A、 |
B、 |
C、 |
D、 |
 如图,∠ACB=∠DBC,AC=DB,求证:∠A=∠D,AB=DC.
如图,∠ACB=∠DBC,AC=DB,求证:∠A=∠D,AB=DC. 如图,已知直线AB,CD,EF相交于点O,∠AOG=90°,∠FOG=32°,∠COE=38°,求∠BOD的度数.
如图,已知直线AB,CD,EF相交于点O,∠AOG=90°,∠FOG=32°,∠COE=38°,求∠BOD的度数.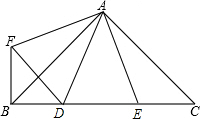 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,过点A作AF⊥AE,且AF=AE,连接BF、EF.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,过点A作AF⊥AE,且AF=AE,连接BF、EF.