题目内容
如图,为了测量某山AB的高度,小明先在山脚下C点测得山顶A的仰角为45°,然后沿坡角为30°的斜坡走100米到达D点,在D点测得山顶A的仰角为30°,求山AB的高度.(参考数据:  ≈1.73)
≈1.73)
【答案】
约为236.5米
【解析】
试题分析:解:过D作DE⊥BC于E,作DF⊥AB于F,设AB=x,

在R t△DEC中,∠DCE=30°,CD=100,
∴DE=50,CE= ,在R t△ABC中,∠ACB=45°,
,在R t△ABC中,∠ACB=45°,
∴BC=x
则AF=AB-BF=AB-DE=x-50
DF="BE=BC+CE=x+" 
在R t△AFD中,∠ADF=30°,tan30°= =
= ,
,
∴ =
= ,
,
∴x= ≈236.5(米),
≈236.5(米),
答:山AB的高度约为236.5米.
考点:三角函数
点评:该题主要考查学生对三角函数值的应用,以及仰角俯角测量方式的意义,是常考题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
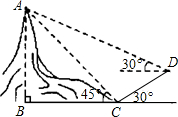 (2012•十堰)如图,为了测量某山AB的高度,小明先在山脚下C点测得山顶A的仰角为45°,然后沿坡角为30°的斜坡走100米到达D点,在D点测得山顶A的仰角为30°,求山AB的高度.(参考数据:
(2012•十堰)如图,为了测量某山AB的高度,小明先在山脚下C点测得山顶A的仰角为45°,然后沿坡角为30°的斜坡走100米到达D点,在D点测得山顶A的仰角为30°,求山AB的高度.(参考数据: ≈1.73)
≈1.73)

 ≈1.73)
≈1.73)