Question

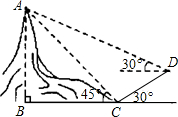（2012•十堰）如图，为了测量某山AB的高度，小明先在山脚下C点测得山顶A的仰角为45°，然后沿坡角为30°的斜坡走100米到达D点，在D点测得山顶A的仰角为30°，求山AB的高度．（参考数据：

3

≈1.73）

Answer 1

分析：易证△ABC是等腰直角三角形，直角△CDE中已知边CD和∠DCE=30°，则三角形的三边的长度可以得到CE，DE的长度，设BC=x，则AE和DF即可用含x的代数式表示出来，在直角△AED中，利用三角函数即可得到一个关于x的方程，即可求得x的值．

解答：解：过D作DE⊥BC于E，作DF⊥AB于F，设AB=x，
在Rt△DEC中，∠DCE=30°，CD=100，
∴DE=50，CE=50

3

在Rt△ABC中，∠ACB=45°，
∴BC=x
则AF=AB-BF=AB-DE=x-50
DF=BE=BC+CE=x+50

3

，
在Rt△AFD中，∠ADF=30°，tan30°=

AF

FD

，
∴

x-50

x+50 3

=

3

3

，
∴x=50（3+

3

）≈236.5，
经检验：x=50（3+

3

）是原分式方程的解．
答：山AB的高度约为236.5米．

点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形，并结合图形利用三角函数解直角三角形．