ƒøƒ⁄»ð
°æƒø°øƒ≥÷÷µÁ¿¬‘⁄ø’÷–ºÐ…Ë ±£¨¡Ω∂Àπ“∆µƒµÁ¿¬œ¬¥π∂ºΩ¸À∆≥…≈◊ŒÔœþ![]() µƒ–Œ◊¥£¨œ÷∞¥≤Ÿ◊˜“™«Û£¨µÁ¿¬◊ÓµÕµ„¿ÎÀÆ∆Ωµÿ√Ê≤ªµ√–°”⁄6√◊£Æ
µƒ–Œ◊¥£¨œ÷∞¥≤Ÿ◊˜“™«Û£¨µÁ¿¬◊ÓµÕµ„¿ÎÀÆ∆Ωµÿ√Ê≤ªµ√–°”⁄6√◊£Æ
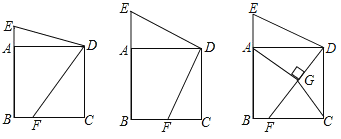
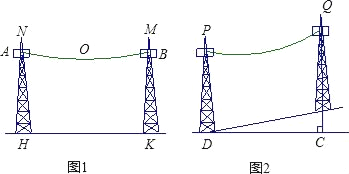
(1)»ÁÕº1£¨»ÙÀÆ∆Ωæý¿Îº‰∏Ù80√◊Ω®‘Ï“ª∏ˆµÁ¿¬À˛÷˘£¨«Û¥ÀµÁ¿¬À˛÷˘”√”⁄πÃ∂®µÁ¿¬µƒŒª÷√¿Îµÿ√Ê÷¡…Ÿ”¶”–∂ý…Ÿ√◊µƒ∏þ∂»£ø
(2)»ÁÕº2£¨»Ù‘⁄“ª∏ˆ∆¬∂»Œ™1£∫5µƒ–±∆¬…œ£¨∞¥ÀÆ∆Ωæý¿Îº‰∏Ù50√◊ºÐ…Ë¡ΩπÃ∂®µÁ¿¬µƒŒª÷√¿Îµÿ√Ê∏þ∂»Œ™20√◊µƒÀ˛÷˘£Æ
¢Ÿ«Û’‚÷÷«Èøˆœ¬‘⁄ ˙÷±∑ΩœÚ…œ£¨œ¬¥πµƒµÁ¿¬”Ζ±∆¬µƒ◊ÓΩ¸æý¿ÎŒ™∂ý…Ÿ√◊£ø
¢⁄’‚÷÷«Èøˆœ¬£¨÷±Ω”–¥≥ˆœ¬¥πµƒµÁ¿¬”εÿ√ʵƒ◊ÓΩ¸æý¿ÎŒ™∂ý…Ÿ√◊£ø
°æ¥∞∏°ø(1) 22√◊£ª(2)¢Ÿ13.48√◊£ª¢⁄17.75√◊£Æ
°æΩ‚Œˆ°ø
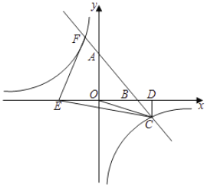
(1)“ÚŒ™ÀÆ∆Ωæý¿Îº‰∏Ù80√◊£¨Àµ√˜◊ÓµÕµ„µƒ∫·◊¯±ÍŒ™40£¨¥˙»Îy=![]() £¨«Û≥ˆ∏þ∂»£¨º”…œ6º¥ø…£ª
£¨«Û≥ˆ∏þ∂»£¨º”…œ6º¥ø…£ª
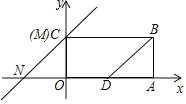
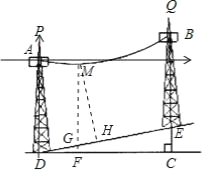
£®2£©“‘µ„DŒ™‘≠µ„£¨DC∑ΩœÚŒ™x÷·’˝∑ΩœÚΩ®¡¢◊¯±Íœµ£¨…Ë≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=![]() x2+bx+c£¨∞—A£®0£¨20£©£¨B(50£¨30)¥˙»Î£¨ø…«Û≥ˆ≈◊ŒÔœþµƒΩ‚Œˆ Ω°£∏˘æðD(0£¨0)°¢E(50£¨10)«Û≥ˆ÷±œþDEµƒΩ‚Œˆ Ω£¨…Ë“ªÃı”Îx÷·¥π÷±µƒ÷±œþx=m”Î≈◊ŒÔœþΩª”⁄M£¨”Ζ±∆¬Ωª”⁄G£¨«Û≥ˆ±Ì æMGæý¿ÎµƒΩ‚Œˆ Ωµƒ◊Ó–°÷µ£¨‘Ÿ◊˜MH°ÕDE”ÎH£¨∏˘æð°˜MGH°◊°˜DEC“‘º∞∆¬∂»1£∫5£¨º¥ø…«Û≥ˆœ¬¥πµƒµÁ¿¬”Ζ±∆¬µƒ◊ÓΩ¸æý¿ÎMHµƒ≥§£¨∏˘æð≈◊ŒÔœþΩ‚Œˆ Ωµƒ◊Ó÷µº¥ø…«Û≥ˆœ¬¥πµÁ¿¬”εÿ√ʵƒ◊ÓΩ¸æý¿Î.
x2+bx+c£¨∞—A£®0£¨20£©£¨B(50£¨30)¥˙»Î£¨ø…«Û≥ˆ≈◊ŒÔœþµƒΩ‚Œˆ Ω°£∏˘æðD(0£¨0)°¢E(50£¨10)«Û≥ˆ÷±œþDEµƒΩ‚Œˆ Ω£¨…Ë“ªÃı”Îx÷·¥π÷±µƒ÷±œþx=m”Î≈◊ŒÔœþΩª”⁄M£¨”Ζ±∆¬Ωª”⁄G£¨«Û≥ˆ±Ì æMGæý¿ÎµƒΩ‚Œˆ Ωµƒ◊Ó–°÷µ£¨‘Ÿ◊˜MH°ÕDE”ÎH£¨∏˘æð°˜MGH°◊°˜DEC“‘º∞∆¬∂»1£∫5£¨º¥ø…«Û≥ˆœ¬¥πµƒµÁ¿¬”Ζ±∆¬µƒ◊ÓΩ¸æý¿ÎMHµƒ≥§£¨∏˘æð≈◊ŒÔœþΩ‚Œˆ Ωµƒ◊Ó÷µº¥ø…«Û≥ˆœ¬¥πµÁ¿¬”εÿ√ʵƒ◊ÓΩ¸æý¿Î.
(1)y=![]() °¡402=16£¨
°¡402=16£¨
16+6=22√◊£ª
πÃ∂®µÁ¿¬µƒŒª÷√¿Îµÿ√Ê÷¡…Ÿ”¶”–22√◊µƒ∏þ∂»£Æ
(2)»ÁÕº£¨¢Ÿ“‘DŒ™◊¯±Í‘≠µ„£¨DC∑ΩœÚŒ™x÷·’˝∑ΩœÚΩ®¡¢÷±Ω«◊¯±Íœµ£Æ
…Ë¥À ±≈◊ŒÔœþΩ‚Œˆ ΩŒ™y=![]() x2+bx+c£¨
x2+bx+c£¨
“◊÷™£∫A£®0£¨20£©£¨B£®50£¨30£©£¨¥˙»ÎΩ‚Œˆ Ωø…«Ûµ√b=-![]() £¨c£Ω20£Æ
£¨c£Ω20£Æ
°ýy=![]() x2©Å
x2©Å![]() x+20£¨
x+20£¨
“◊«Ûµ√–±∆¬À˘‘⁄÷±œþµƒΩ‚Œˆ ΩŒ™£∫y=![]() x£¨
x£¨
…Ë“ªÃı”Îx÷·¥π÷±µƒ÷±œþx=m”Î≈◊ŒÔœþΩª”⁄M£¨”Ζ±∆¬Ωª”⁄G£Æ
‘Ú£∫MG=![]() m2©Å
m2©Å![]() m+20©Å
m+20©Å![]() m£Ω
m£Ω![]() (m©Å25)2+13.75£¨
(m©Å25)2+13.75£¨
°ýµ±m=25 ±£¨MGµƒ◊Ó–°÷µŒ™13.75£Æ◊˜MH°ÕDE”ÎH£Æ
MH=13.75°¬![]() °¡5=13.48£®√◊£©£¨
°¡5=13.48£®√◊£©£¨
º¥‘⁄ ˙÷±∑ΩœÚ…œ£¨œ¬¥πµƒµÁ¿¬”Ζ±∆¬µƒ◊ÓΩ¸æý¿ÎŒ™13.48√◊£¨
¢⁄°þy£Ω![]() x2©Å
x2©Å![]() x+20£Ω
x+20£Ω![]() (x-15)2+17.75£¨
(x-15)2+17.75£¨
°ýœ¬¥πµƒµÁ¿¬”εÿ√ʵƒ◊ÓΩ¸æý¿ÎŒ™17.75√◊£Æ
π ¥∞∏Œ™£∫(1) 22√◊£ª(2)¢Ÿ13.48√◊£ª¢⁄17.75√◊£Æ