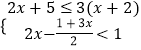Question

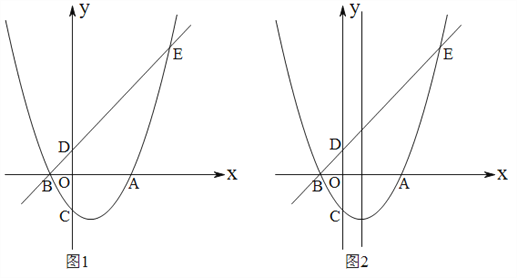
【题目】已知，如图1：抛物线 交轴于、两点，交轴于点，对称轴为直线，且过点.

（1）求出抛物线的解析式及点坐标，

（2）点， ，作直线交抛物线于另一点，点是直线下方抛物线上的点，连接、，求的面积的最大值，并求出此时点的坐标；

（3）点、是抛物线对称轴上的两点，且已知（， ），（， ），当为何值时，四边形周长最小？并求出四边形周长的最小值，请说明理由.

Answer 1

【答案】（1）；（2） ， ；（3），周长最小值是，理由见解析

【解析】试题分析：（1）根据函数图象过点和对称轴方程列出方程组求解即可；

（2）求出点B的坐标，再求出直线BD的解析式，与抛物线联立方程组即可求出点E坐标，根据三角形面积的计算公式得出表示三角形面积的二次函数，求出最大值即可；

（3）在四边形ANME中，MN，AE是定值，四边形周长最小，即AN+ME最小.利用轴对称即可求解.

试题解析：（1）由题可得：

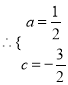
（2）当y=0时，

∴

∴A（3，0），B（-1，0）

∵D（0，1）

∴直线BD：y=x+1

∴解方程得：

∴E（5，6）

过点F作FG⊥x轴交直线BE于点G

设F（m， ），-1<m<5，G（m，m+1）

∴GF=

∴SΔDEF=

∵<0

∴i当m=2时，ΔDEF的面积有最大值，最大值是

∴F（2， ）

（3）∵A（3，0），E（5，6）

∴AE=

∵M（1，a+2），N（1，a）

∴MN=2

∴当ME+AN的值最小时，四边形AEMN的周长最小，

∵点和点B关于直线x=1对称，将点向下平移2个单位长度得到点，

连结BE交直线x=1于点N，再将点N向上平移2个单位长度得到点M，连结AN、ME、AE.