题目内容
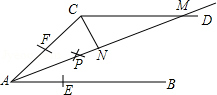
 如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于
如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于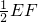 的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为
的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为
- A.100°
- B.110°
- C.120°
- D.130°
D
分析:连接PE、PF,根据SSS证△AFP≌△AEP,推出∠FAP=∠EAP,求出∠FAP=∠EAP=∠C=25°,根据三角形内角和定理求出即可.
解答: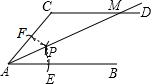
解:连接PF、PE,
由作法可知:AF=AE,PF=PE,
∵在△AFP和△AEP中
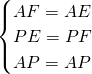
∴△AFP≌△AEP(SSS),
∴∠FAP=∠EAP,
∵AB∥CD,
∴∠BAM=∠CMA=25°,
∴∠CAP=25°,
∴∠C=180°-∠CMA-∠CAP=130°,
故选D.
点评:本题考查了平行线性质,三角形内角和定理,全等三角形的性质和判定的应用,主要考查学生的推理能力.
分析:连接PE、PF,根据SSS证△AFP≌△AEP,推出∠FAP=∠EAP,求出∠FAP=∠EAP=∠C=25°,根据三角形内角和定理求出即可.
解答:

解:连接PF、PE,
由作法可知:AF=AE,PF=PE,
∵在△AFP和△AEP中
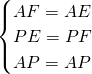
∴△AFP≌△AEP(SSS),
∴∠FAP=∠EAP,
∵AB∥CD,
∴∠BAM=∠CMA=25°,
∴∠CAP=25°,
∴∠C=180°-∠CMA-∠CAP=130°,
故选D.
点评:本题考查了平行线性质,三角形内角和定理,全等三角形的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
 (2012•绍兴)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
(2012•绍兴)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于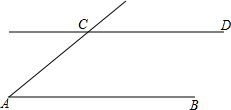 (2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
(2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于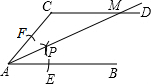 如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于
如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于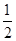 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。