题目内容
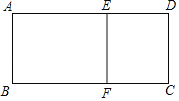
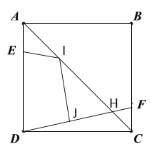
【题目】如图，正方形
边长为
，
，
分别为线段
，
上一点，且
，
，
与
相交于
，
为线段
上一点（不与端点重合），
为线段
上一点（不与端点重合），则
的最小值为（ ）
A.
B.
C.
D.
【答案】C
【解析】
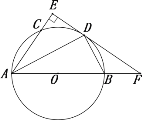
作点E关于AC的对称点K，EI+IJ=KI+KJ，当EJ⊥DF时
有最小值，如下图所示，延长KJ交DC于N点，过N作NM∥AD，得到△KMN≌△FCD，再由△DJ0N∽△DCF求出J0N，最后KN减去J0N即为所求.
解：如图，作点E关于AC的对称点K，当EJ⊥DF时EI+IJ有最小值为KJ0，此时设KN与DF、CD的交点分别为J0和N点，过N点作MN∥AD交AB于点M.
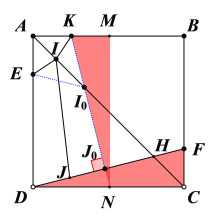
∵∠KND+∠FDC=90°，
∠DFC+∠FDC=90°
∴∠KND=∠DFC
又∵AB∥CD
∴∠MKN=∠KND=∠DFC
在△MKN和△CFD中
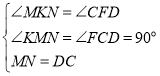，∴△MKN≌△CFD(AAS)
∴
,
又△DJ0N∽△DCF
∴
，代入数据：
，得
∴
.
故答案为：C.
练习册系列答案
相关题目
【题目】表中所列
、
的7对值是二次函数
图象上的点所对应的坐标，其中
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息，有以下4个判断：①
；②
；③当
时，的值是
；④
；其中判断正确的是（ ）
A.①②③B.①②④C.①③④D.②③④
【题目】小魏探究学习函数的经验，对函数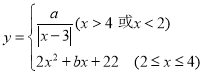
的图像与性质进行了研究，下面是小魏的探究过程，请补充完整．
（1）下表是
与
的几组对应值：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请直接写出：
_______，
______，
_______．
（2）画出该函数图像．
（3）写出该函数的一条性质：_______________．
（4）一次函数
与该函数图像至少有三个交点，则
的范围_______．
