题目内容
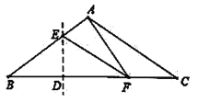
【题目】如图1,折叠矩形![]() ,具体操作:①点
,具体操作:①点![]() 为
为![]() 边上一点(不与
边上一点(不与![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直线折叠,
所在的直线折叠,![]() 点的对称点为
点的对称点为![]() 点;②过点
点;②过点![]() 对折
对折![]() ,折痕
,折痕![]() 所在的直线交
所在的直线交![]() 于点
于点![]() 、
、![]() 点的对称点为
点的对称点为![]() 点.
点.
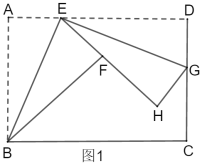
(1)求证:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
①点![]() 在移动的过程中,求
在移动的过程中,求![]() 的最大值.
的最大值.
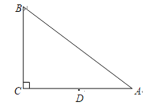
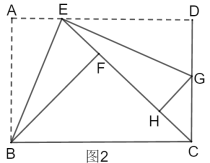
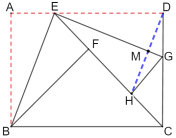
②如图2,若点![]() 恰在直线
恰在直线![]() 上,连接
上,连接![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)①![]() 的最大值为
的最大值为![]() ;②
;②![]()
【解析】
(1)由矩形和折叠的性质可知![]() ,然后通过
,然后通过![]() 得出
得出![]() ,则可证明结论;
,则可证明结论;
(2)设![]() ,则
,则![]() ,根据相似三角形的性质有
,根据相似三角形的性质有![]() ,进而可表示出DG的长度,然后利用二次函数的性质求最大值即可;
,进而可表示出DG的长度,然后利用二次函数的性质求最大值即可;
(3)连接DH,设![]() ,则
,则![]() ,先通过勾股定理求出CF,CE,进而在
,先通过勾股定理求出CF,CE,进而在![]() 中,利用勾股定理求出x的值,进而可求DE,DG,EG的长度,然后利用
中,利用勾股定理求出x的值,进而可求DE,DG,EG的长度,然后利用![]() 求出DM的长度,最后利用
求出DM的长度,最后利用![]() 即可求解.
即可求解.
(1)∵四边形ABCD是矩形,
∴![]() .
.
由折叠的性质可知, ![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ∽
∽![]() ;
;
(2)①设![]() ,则
,则![]() ,
,
由(1)知:![]() ∽
∽![]()
∴![]() ,
,
∴![]() (
(![]() ),
),
故当![]() 时,
时,![]() 取到最大值为
取到最大值为![]() ;
;
②连接DH,
设![]() ,则
,则![]() ,
,
由折叠的性质可知,BF=AB=3,BC=5,
在![]() 中,
中,
![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴DE=4.
由①知:![]() ,
,
∴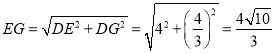 .
.
∵![]() 垂直平分DH,
垂直平分DH,
∴DH=2DM,
又∵![]() ,
,
∴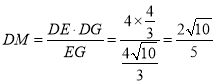 ,
,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?