Question

【题目】已知中，，为线段上一点（不与，重合），点为线段上一点，，设，．

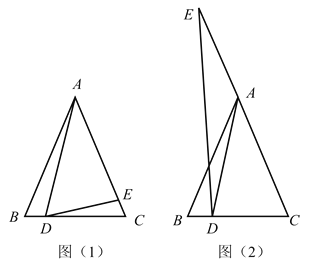
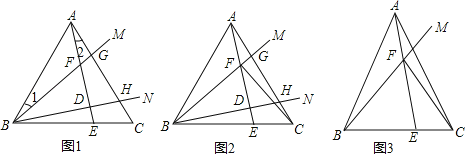
（1）如图（1），

①若，，则____________，_______________．

②若，，则____________，______________．

③写出与的数量关系，并说明理由；

（2）如图（2），当点在的延长线上时，其它条件不变，请直接写出与的数量关系．

Answer 1

【答案】（1）①；；②；；③，理由详见解析；（2）

【解析】

（1）①由可得，由等腰三角形两底角相等及三角形内角和定理可求出的度数，相减即得；

②由可得，由等腰三角形两底角相等及三角形内角和定理可求出的度数，相减即得；

③由外角的性质可得，可表示出，由等量代换可得结论；

（2）由外角的性质可得，进一步可表示出，在中，由三角形内角和定理及等腰三角形的性质可得，在中，由三角形内角和定理可得与的数量关系．

（1）①，

且，

，

，

所以，；

②，

且，

，

，

所以，；

③解：，

理由是：，

，

（3）.