题目内容
如图正三角形
边长为2，
分别是
上的点，且
，设
的面积为
，
的长为
，则的最小值为_____________。
【答案】
【解析】根据题意，有AE=BF=CG，且正三角形ABC的边长为2，故BE=CF=AG=2-x；
故△AEG、△BEF、△CFG三个三角形全等．在△AEG中，AE=x，AG=2-x．
则S△AEG=
AE×AG×sinA=x（2-x）；
故y=S△ABC-3S△AEG=
-3×x（2-x）=（3x2-6x+4）=
．当x=1
时，y取得最小值为。
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
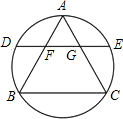如图，边长为12的正三角形ABC内接于圆，弦DE∥BC分别交AB，AC于F，G，若AF长x，DF长y都是正整数，则y的值为（ ）
边长为2，
分别是
上的点，且
，设
的面积为
，
的长为
，则