题目内容
 (2013•自贡)如图,已知A、B是反比例函数y=
(2013•自贡)如图,已知A、B是反比例函数y=| k |
| x |
分析:通过两段的判断即可得出答案,①点P在AB上运动时,此时四边形OMPN的面积不变,可以排除B、D;②点P在BC上运动时,S减小,S与t的关系为一次函数,从而排除C.
解答:解:①点P在AB上运动时,此时四边形OMPN的面积S=K,保持不变,故排除B、D;
②点P在BC上运动时,设路线O→A→B→C的总路程为l,点P的速度为a,则S=OC×CP=OC×(l-at),因为l,OC,a均是常数,
所以S与t成一次函数关系.故排除C.
故选A.
②点P在BC上运动时,设路线O→A→B→C的总路程为l,点P的速度为a,则S=OC×CP=OC×(l-at),因为l,OC,a均是常数,
所以S与t成一次函数关系.故排除C.
故选A.
点评:本题考查了动点问题的函数图象,解答此类题目并不需要求出函数解析式,只要判断出函数的增减性,或者函数的性质即可,注意排除法的运用.

练习册系列答案
相关题目
 (2013•自贡)如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为( )
(2013•自贡)如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为( ) (2013•自贡)如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=
(2013•自贡)如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG= (2013•自贡)如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )
(2013•自贡)如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )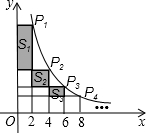 (2013•自贡)如图,在函数
(2013•自贡)如图,在函数 (2013•自贡)如图,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=
(2013•自贡)如图,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=