题目内容
（本题满分12分）如图，直线l1的解析表达式为：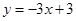
，且l1与x轴
交于点D，直线l2经过点A，B，直线l1，l2交于点C．
小题1:（1）求直线l2的函数关系式；
小题2:（2）求△ADC的面积；
小题3:（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．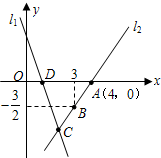
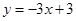，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．
小题1:（1）求直线l2的函数关系式；
小题2:（2）求△ADC的面积；
小题3:（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．
小题1:解：⑴设直线l2的函数关系式为y=kx＋b
∵当x＝4时，y＝0；当x＝3时，y＝
∴
，∴
∴直线l2的函数关系式为
小题2:⑵由直线l1：
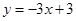,直线l2：可求得D(1,0)，C（2，-3）………………8分
∴
小题3:⑶D点坐标是（5，-3），（3,3）（-1，-3）
略
练习册系列答案
相关题目
分别与x轴，y轴交于点C、D，与反比例函数
的图象交于点A、B.过点A 作AE⊥y轴与点E，过点B作BF⊥x轴与点F，连结EF，下列结论：1AD＝BC；2EF∥AB；3四边形AEFC是平行四边形；4
.其中正确的个数是（ ▲ ）
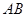分别与
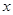轴、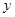
轴交于点A（0,3）和点B（-1,0），求直线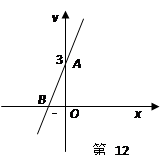
的图像经过 一、二、四象限，则m的取值范围是 ．
的大致图象是（ ）
，y）从M（1，0）出发，沿由A（-1，1），B（-1，-1），C（1，-1），D（1，1）四点组成的正方形边线（如图①）按一定方向运动。图②是P点运动的路程s（个单位）与运动时间
（秒）之间的函数图象，图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.