题目内容
如图,点E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
(1) 试判断四边形AECF的形状;
(2) 若AE=BE,∠BAC=90°,求证:四边形AECF是菱形.
 |
(1)四边形AECF为平行四边形.
∵□ABCD,∴AD=BC,AD∥BC,
又∵BE=DF,∴AF=CE,
∴四边形AECF为平行四边形
(2)证明:∵AE=BE,∴∠B=∠BAE
又∵∠BAC=90°,∴∠B+∠BCA=90°,∠CAE+∠BAE=90°
∴∠BCA=∠CAE
∴AE=CE,又∵四边形AECF为平行四边形,
∴四边形AECF是菱形

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
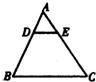 17、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长:△ABC的周长=
17、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长:△ABC的周长=
 (2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
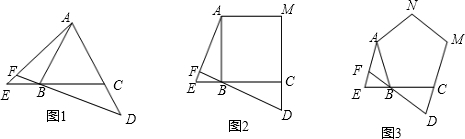
(2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( ) 如图,点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB延长线交于AE于点F,则∠AFB的度数是
如图,点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB延长线交于AE于点F,则∠AFB的度数是