Question

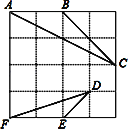
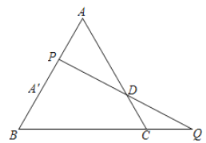
【题目】如图，等边的边长为5，点在边上，点为延长线一点，连结交于，点关于直线的对称点恰好落在边上，当时，的长为（ ）

A.1.5B.C.D.

Answer 1

【答案】C

【解析】

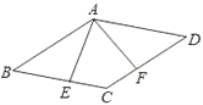
过P作PM∥BC交AC于M，证出△APM为等边三角形，得出PA=PM=AM，证明△PMD≌△QCD (AAS)得出PD=QD，证明△AA D是等边三角形，得出∠AAD=60°=∠B，证出AD// BC，得出AB=PA=PA，即可得出答案．

解：过P作PM// BC交AC于M，如图所示：

∵三边形ABC是等边三角形，
∴∠A=∠B=∠ACB=60° ，PM // BC，
∴∠APM= ∠ B=60°，∠AMP=∠ACB=60°，∠PMD=∠QCD，
∴△APM为等边三角形

∴PA=PM= AM，
∵PA=CQ ，
∴ PM=CQ ，
在△PMD和△QCD中，

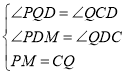
∴△PMD≌△QCD (AAS)
∴PD=QD，
∵点A关于直线PQ的对称点A恰好落在AB边上，
∴PA=PA，∠APD=90° ，

∴∠ADP=30°
∴AP=AD，

∵PA=AM

∴AA=AD，PA=MD

△AAD是等边三角形，
∴∠AAD=60°=∠B，
∴AD// BC，
∴PD=QD，
∴AB=PA=PA，

∴AB=AB=
故选：C