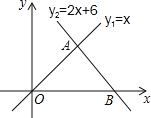题目内容
【题目】要在马路边设一个共享单车投放点，向
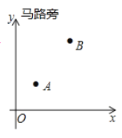
两家公司提供服务，投放点应设在什么地方，才能使从到它的距离之和最短？小明根据实际情况，以马路为
轴建立了如图所示的平面直角坐标系，
点的坐标为
，
点的坐标为
，则从两点到投放点距离之和的最小值是__________，投放点的坐标是__________．
【答案】
【解析】
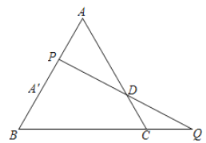
作点A关于y轴的对称点A′，连接BA′交y轴于P，连接PA，此时PA+PB的值最小．
解：作点A关于y轴的对称点A′，连接BA′交y轴于P，连接PA，此时PA+PB的值最小．
∵A（1，2），A与A′关于y轴对称，
∴A′（-1，2），
∵B（4，7），
设直线BA′的解析式为y=kx+b，
则有
，
解得：
，
∴直线BA′的解析式为：y=x+3，
∴P（0，3），
∵PA+PB=PA′+PB=BA′=
，
故答案为：，（0，3）．
练习册系列答案
相关题目
