Question

【题目】阅读下面材料：

在数学课上，老师提出如下问题：

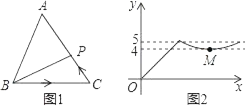
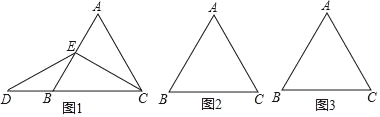
已知：如图1△ABC，尺规作图：求作∠APC＝∠ABC.

甲、乙两位同学的主要作法如下：

甲同学的主要作法，如图甲：①作∠CAD＝∠ACB，且点D与点B在AC的异侧；②在射线AD上截取AP＝CB，连结CP.所以∠APC＝∠ABC.

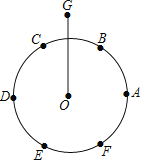
乙同学的主要作法，如图乙：①作线段BC的垂直平分线a；②作线段AB的垂直平分线b，与直线a交于点O；③以点O为圆心，OA为半径作⊙O；④在上取一点P（点P不与点A，B，C重合），连结AP，CP.所以∠ACP＝∠ABC.

老师说：“两位同学的作法都是正确的.”

请你选择一位同学的作法，并说明这位同学作图的依据.

我选择的是_________的作法，这样作图的依据是_________.

Answer 1

【答案】甲 内错角相等，两直线平行；一组对边平行且相等的四边形是平行四边形；平行四边形对角相等

【解析】

甲：由内错角相等，两直线平行；一组对边平行且相等的四边形是平行四边形；平行四边形对角相等可得；

乙：由线段垂直平分线上的点到这条线段两个端点的距离相等；圆的确定；同弧所对的圆周角相等可得.

解：甲、∵∠CAD＝∠ACB，

∴AD∥BC，

又∵AP＝CB，

∴四边形ABCP是平行四边形，

∴∠B＝∠APC，

故甲作法的依据为：内错角相等，两直线平行；一组对边平行且相等的四边形是平行四边形；平行四边形对角相等.

乙、∵a为AB的中垂线、b为BC的中垂线，且交点为O，

∴OA＝OB＝OC，

∴点A、B、C在以O为圆心、OA为半径的圆上，

∴∠APC＝∠ABC，

故乙作法的依据是：线段垂直平分线上的点到这条线段两个端点的距离相等；圆的确定；同弧所对的圆周角相等.

故答案为：甲、内错角相等，两直线平行；一组对边平行且相等的四边形是平行四边形；平行四边形对角相等.