题目内容
如图，⊙O1与⊙O2外切于点D，过D点的直线交OO2于A，交⊙O1于B，∠AO2D=100°，点C是⊙O1上优弧 | DE |
50°
50°
．分析：连接DO1，BO1，利用圆的半径相等得到∠ADO2的度数，从而得到∠BO1D=100°，利用同弧所对的圆周角是圆心角的一半求解即可．
解答：
解：如图，连接DO1，BO1，
∵∠AO2D=100°，
∴∠ADO2=
（180°-100°）=
×80°=40°，
∴∠BDO1=40°
∴∠BO1D=100°，
∴∠DCB=
∠BO1D=50°，
故答案为：50°．
解：如图，连接DO1，BO1，∵∠AO2D=100°，
∴∠ADO2=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BDO1=40°
∴∠BO1D=100°，
∴∠DCB=
| 1 |
| 2 |
故答案为：50°．
点评：本题考查了相切两圆的性质，解题的关键是了解两圆相切时，两圆的连心线经过两圆的切点．
练习册系列答案
相关题目
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=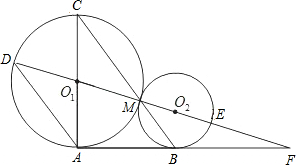
已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
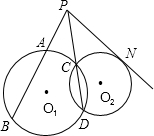如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=
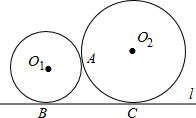已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
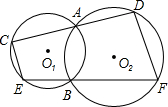已知如图：⊙O1与⊙O2相交于AB两点，过点A、B的直线分别与⊙O1交于C、E，与⊙O2交于D、F，连接CE、DF．