题目内容
 如图,等边三角形ABC中,AB=4,点P是AB上的一个动点(点P可以与点A重合,但不与点B重合),过点P作PE⊥BC,垂足为,过点E作EF⊥AC,垂足为F,过点F作FQ⊥AB,垂足为Q,设BP=x,AQ=y.
如图,等边三角形ABC中,AB=4,点P是AB上的一个动点(点P可以与点A重合,但不与点B重合),过点P作PE⊥BC,垂足为,过点E作EF⊥AC,垂足为F,过点F作FQ⊥AB,垂足为Q,设BP=x,AQ=y.
(1)写出y与x之间的函数关系式及自变量x的取值范围;
(2)当BP的长等于多少时,点P与点Q重合;
(3)用x的代数式表示PQ的长(不必写出解题过程).
 解:(1)PE⊥BC,EF⊥AC,FQ⊥AB,
解:(1)PE⊥BC,EF⊥AC,FQ⊥AB,∠A=∠B=∠C=60°,设BP=x,
∴BE=
 ,EC=4-
,EC=4- ,CF=2-
,CF=2- ,
,AF=4-2+
 =2+
=2+ ,
,∵△BEP∽△AQF,
∴
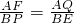 ,
,∴AQ=1+
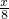 ,
,∴y=1+
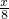 (0<x≤4);
(0<x≤4);(2)当x+y=4,x+1+
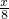 =4,
=4,∴
 x=3,
x=3,∴x=
 ,
,故BP为
 时,P与Q重合;
时,P与Q重合;(3)PQ=

 ,
,PQ=

 .
.分析:(1)设BP=x,利用等边三角形中,三个角均为60°,三边长相等,逐步求出BE,EC,CF,AF的长,利用△BEP∽△AQF,对应边成比例,求出AP与AQ之间的关系;
(2)点P与点Q重合时,有AQ+AP=AB,代入关系式求解,
(3)根据题意及(1)(2)即可推理得出答案.
点评:本题主要考查了利用锐角三角函数的概念,逐步找到x与y关系,同时考查了相似三角形对应边成比例的性质,比较综合,难度较大.

练习册系列答案
相关题目
 已知:如图,等边三角形AOB的顶点A在反比例函数y=
已知:如图,等边三角形AOB的顶点A在反比例函数y= 如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则
如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则 已知:如图,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
已知:如图,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O. 如图,等边三角形ABC的边长为a,若D、E、F、G分别为AB、AC、CD、BF的中点,则△BEG的面积是( )
如图,等边三角形ABC的边长为a,若D、E、F、G分别为AB、AC、CD、BF的中点,则△BEG的面积是( )