题目内容
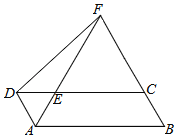
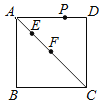
【题目】如图,在正方形ABCD中,AB=4,E、F是对角线AC上的两个动点,且EF=2,P是正方形四边上的任意一点.若△PEF是等边三角形,则符合条件的P点共有_____个,此时AE的长为_____.
【答案】4 ![]() 或
或![]()
【解析】
当点P在AD上时,过点PH⊥EF于H,由等边三角形的性质可求PH=![]() ,由正方形的性质可求∠DAC=45°,AC=
,由正方形的性质可求∠DAC=45°,AC=![]() AB=4
AB=4![]() ,可得AH=PH,可求AE=
,可得AH=PH,可求AE=![]() ﹣1,同理可求点P在AB,CD,BC上时,AE的值,即可求解.
﹣1,同理可求点P在AB,CD,BC上时,AE的值,即可求解.
解:如图,当点P在AD上时,过点PH⊥EF于H,

∵△PEF是等边三角形,PH⊥EF,
∴∠PEF=60°,PE=PF=EF=2,EH=FH=1,
∴PH=![]() ,
,
∵四边形ABCD是正方形,AB=4,
∴∠DAC=45°,AC=![]() AB=4
AB=4![]() ,
,
∵PH⊥AC,
∴∠APH=∠PAH=45°,
∴AH=PH=![]() ,
,
∴AE=![]() ﹣1,
﹣1,
同理可得:当点P在AB上时,AE=![]() ﹣1,
﹣1,
当点P在CD或BC上时,AE=4![]() ﹣2﹣(
﹣2﹣(![]() ﹣1)=4
﹣1)=4![]() ﹣
﹣![]() ﹣1,
﹣1,
故答案为:4,![]() 或
或![]() .
.

 世纪百通期末金卷系列答案
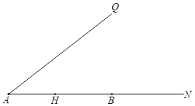
世纪百通期末金卷系列答案【题目】如图,点M是⊙O直径AB上一定点,点C是直径AB上一个动点,过点![]() 作
作![]() 交⊙O于点
交⊙O于点![]() ,作射线DM交⊙O于点N,连接BD.
,作射线DM交⊙O于点N,连接BD.

小勇根据学习函数的经验,对线段AC,BD,MN的长度之间的数量关系进行了探究.
下面是小勇的探究过程,请补充完整:
(1)对于点C在AB的不同位置,画图,测量,得到了线段AC,BD,MN的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AC/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
BD/cm | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | 0.00 |
MN/cm | 4.00 | 3.27 | 2.83 | 2.53 | 2.31 | 2.14 | 2.00 |
在AC,BD,MN的长度这三个量中,如果选择________的长度为自变量,那么________的长度和________的长度为这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中确定的函数的图象;

(3)结合函数图象解决问题:当BD=MN时,线段AC的长度约为_____cm(结果精确到0.1).
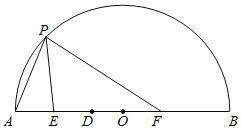
【题目】如图,D是直径AB上一定点,E,F分别是AD,BD的中点,P是![]() 上一动点,连接PA,PE,PF.已知AB=6cm,设A,P两点间的距离为xcm,P,E两点间的距离为y1cm,P,F两点间的距离为y2cm.
上一动点,连接PA,PE,PF.已知AB=6cm,设A,P两点间的距离为xcm,P,E两点间的距离为y1cm,P,F两点间的距离为y2cm.
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0.97 | 1.27 |
| 2.66 | 3.43 | 4.22 | 5.02 |
y2/cm | 3.97 | 3.93 | 3.80 | 3.58 | 3.25 | 2.76 | 2.02 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
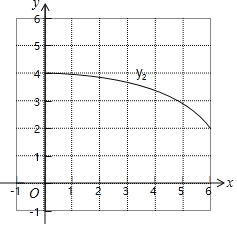
(3)结合函数图象,解决问题:当△PEF为等腰三角形时,AP的长度约为 cm.