题目内容
如图，点A、B是反比例函数
（x＞0）图象上的两个点，在△AOB中，OA=OB，BD垂直于x轴，垂足为D，且AB=2BD，则△AOB的面积为________．
3
分析：作等腰三角形底边上的高，利用等腰三角形的性质和已知条件得到两个三角形全等，由此可以得到△AOB的面积是△OBD的2倍，进而求得△OAB的面积．
解答：
解：作OC⊥AB于C点，
∵OA=OB，
∴AC=CB，
∵AB=2BD，
∴BC=BD，
∵∠BDO=∠BCO=90°，OB=OB，
∴△OCB≌△ODB，
∵S△OBD=
，
∴S△OAB=2S△OBC=2×=3．
故答案为：3．
点评：本题考查了反比例函数的综合知识，解题的关键是作出等腰三角形的高，利用直角三角形的全等的判定的方法判定直角三角形全等，进而求得等腰三角形的面积．
分析：作等腰三角形底边上的高，利用等腰三角形的性质和已知条件得到两个三角形全等，由此可以得到△AOB的面积是△OBD的2倍，进而求得△OAB的面积．
解答：
解：作OC⊥AB于C点，∵OA=OB，
∴AC=CB，
∵AB=2BD，
∴BC=BD，
∵∠BDO=∠BCO=90°，OB=OB，
∴△OCB≌△ODB，
∵S△OBD=
，∴S△OAB=2S△OBC=2×
=3．故答案为：3．
点评：本题考查了反比例函数的综合知识，解题的关键是作出等腰三角形的高，利用直角三角形的全等的判定的方法判定直角三角形全等，进而求得等腰三角形的面积．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
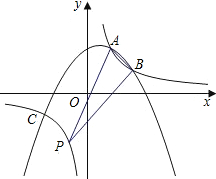如图，抛物线y=ax2+bx+c经过点A（1，2）、B（2，1）和C（-2，-1）三点．
如图，△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形，点P1、P2、P3、…、P100在反比列函数
如图所示，点P（a，-2a）是反比列函数
图象上一点，过点A作x轴的垂线。垂足为 B点.若OA=
，则△AOB的周长为（ ）。