题目内容
【题目】如图,已知二次函数y= ![]() x2﹣
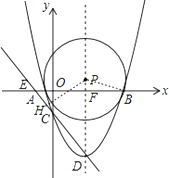
x2﹣ ![]() x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
【答案】(4,0)或(4, ![]() )
)
【解析】解:当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣3=0,解得x1=﹣1,x2=9,则A(﹣1,0),B(9,0),
x﹣3=0,解得x1=﹣1,x2=9,则A(﹣1,0),B(9,0),
当x=0时,y= ![]() x2﹣
x2﹣ ![]() x﹣3=﹣3,则C(0,﹣3),
x﹣3=﹣3,则C(0,﹣3),
∵y= ![]() x2﹣
x2﹣ ![]() x﹣3=
x﹣3= ![]() (x﹣4)2﹣
(x﹣4)2﹣ ![]() ,
,
∴抛物线的对称轴为直线x=4,D点坐标为(4,﹣ ![]() ),
),
设直线CD的解析式为y=kx+b,
把C(0,﹣3),D(4,﹣ ![]() )代入得
)代入得 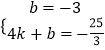 ,解得
,解得 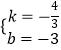 ,
,
∴直线CD的解析式为y=﹣ ![]() x﹣3,
x﹣3,
过P点作PH⊥直线CD于H,连结PB,CD交x轴于E点,抛物线的对称轴交x轴于F点,如图,则F(4,0),E(﹣ ![]() ,0),
,0),
∴EF=4﹣(﹣ ![]() )=
)= ![]() ,FB=
,FB= ![]() ,
,
∴DE= ![]() =
= ![]() ,
,
设P(4,t),则PD=t+ ![]() ,PB=
,PB= ![]() =
= ![]() ,
,
∵以P为圆心的圆经过A,B两点,并且和直线CD相切,
∴PH=PB= ![]() ,
,
∵∠PDH=∠EDF,
∴Rt△DPH∽Rt△DEF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
整理得8t2﹣75t=0,解得t1=0,t2= ![]() ,
,
∴P点坐标为(4,0)或(4, ![]() ).
).
所以答案是(4,0)或(4, ![]() ).
).
【考点精析】掌握二次函数的性质和切线的性质定理是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

 口算能手系列答案
口算能手系列答案