题目内容
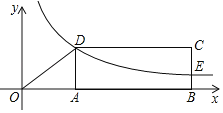
【题目】如图，在平面直角坐标系
中，直线
与
轴，
轴分别相交于点
．点
是轴上动点，点从点
出发向原点O运动，点
在点右侧，
．过点作
于点
将
沿直线
翻折，得到
连接
．设
与
重合部分面积为
求：
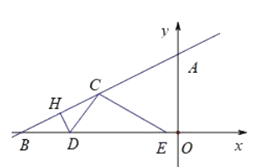
（1）求线段
的长(用含
的代数式表示)；
（2）求
关于的函数解析式，并直接写出自变量的取值范围．
【答案】（1）
；（2）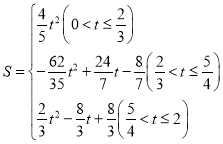
【解析】
（1）先根据直线
求得点A、B的坐标，利用勾股定理求得AB的长，进而可求得
，由翻折知
，
，最后根据
求得
，即可求得BC的长；
（2）分类讨论：当
时，当
时，当
时，分别画出相应图形，然后利用相似三角形的性质分别表示出对应的底和高，进而可得
关于
的函数解析式即可．
解：
∵直线与
轴，
轴分别相交于点
，
点
，
由勾股定理得
，
在直角
中，，
由翻折知：，，
，
，
，
当时，
过点
做
于点
，
，
，
，
当时，
设
交
于点
，
，
由勾股定理得
，
，
，
，
，
，
，
，
，
，
当时，
设
交于点
，
，
，
，
，
综上所述，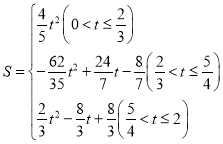
练习册系列答案
相关题目
【题目】某公司销售甲、乙两种品牌的投影仪，这两种投影仪的进价和售价如下表所示：
甲 | 乙 | |
进价（元/套） | 3000 | 2400 |
售价（元/套） | 3300 | 2800 |
该公司计划购进两种投影仪若干套，共需66000元，全部销售后可获毛利润9000元．
（1）该公司计划购进甲、乙两种品牌的投影仪各多少套？
（2）通过市场调研，该公司决定在原计划的基础上，减少甲种投影仪的购进数量，增加乙种投影仪的购进数量，已知乙种投影仪增加的数量是甲种投影仪减少的数量的2倍。若用于购进这两种投影仪的总资金不超过75000元，问甲种投影仪购进数量至多减少多少套？
