Question

20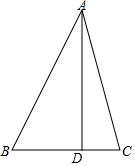．已知△ABC中，AD⊥BC于点D，∠BAC=45°，BD=6，CD=4，
（1）画出△ABC的外接圆（尺规作图，不写作法，保留痕迹）
（2）求△ABC的外接圆半径与AD长．

Answer 1

分析 （1）分别作出边BC、AC的中垂线，交点为O，以点O为圆心、OA为半径画圆即可得；
（2）作OE⊥AD、OF⊥BC，由圆周角定理得出△BOC为等腰直角三角形且BC=10，从而得OB=OC=$\frac{\sqrt{2}}{2}$BC=5$\sqrt{2}$；根据垂径定理可得BF=CF=OF=$\frac{1}{2}$BC=5，证四边形OEDF是矩形可得DE=OF=5、OE=DF=CF-CD=1，利用勾股定理可求得AE的长，即可得出答案．

解答 解：（1）如图所示，⊙O即为所求；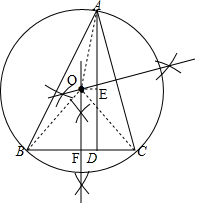


（2）过点O作OE⊥AD于点E，作OF⊥BC于点F，连接OA、OB、OC，
∵∠BAC=45°，
∴∠BOC=90°，
∵OB=OC，且BD=6、CD=4，
∴△BOC为等腰直角三角形，且BC=10，
则OB=OC=$\frac{\sqrt{2}}{2}$BC=5$\sqrt{2}$，即△ABC外接圆半径为5$\sqrt{2}$；
∵Rt△BOC中，BC=10，OF⊥BC，
∴BF=CF=OF=$\frac{1}{2}$BC=5，
∵∠OED=∠OFD=∠EDF=90°，
∴四边形OEDF是矩形，
∴DE=OF=5，OE=DF=CF-CD=1，
在Rt△OAE中，∵AE=$\sqrt{O{A}^{2}-O{E}^{2}}$=$\sqrt{（5\sqrt{2}）^{2}-{1}^{2}}$=7，
∴AD=AE+DE=12．

点评 本题主要考查作图-复杂作图，掌握三角形外接圆的性质及圆周角定理、垂径定理、等腰直角三角形的判定与性质及勾股定理、矩形的判定与性质是解题的关键．