题目内容
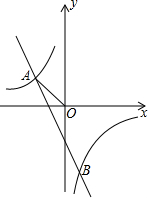 (2013•达州)已知反比例函数y=
(2013•达州)已知反比例函数y=| k1 |
| 3x |
| 1 |
| 3 |
(1)求反比例函数和一次函数的表达式;
(2)设点C在y轴上,且与点A、O构成等腰三角形,请直接写出点C的坐标.
分析:(1)将点A(-1,a)、B(
,-3)代入反比例函数y=
中得:-3×
=(-1)×a=k1,可求k1、a;再将点A(-1,a)、B(
,-3)代入y2=k2x+m中,列方程组求k2、m即可;
(2)分三种情况:①OA=OC;②AO=AC;③CA=CO;讨论可得点C的坐标.
| 1 |
| 3 |
| k1 |
| 3x |
| 1 |
| 3 |
| 1 |
| 3 |
(2)分三种情况:①OA=OC;②AO=AC;③CA=CO;讨论可得点C的坐标.
解答:解:(1)∵反比例函数y=
的图象经过B(
,-3),
∴k1=3×
×(-3)=-3,
∵反比例函数y=
的图象经过点A(-1,a),
∴a=1.
由直线y2=k2x+m过点A,B得:
,
解得
.
∴反比例函数关系式为y=-
,一次函数关系式为y=-3x-2;
(2)点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,-
)或(0,
)或(0,2)或(0,1).
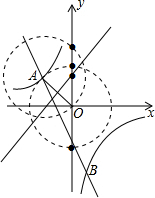
如图,线段OA的垂直平分线与y轴的交点,有1个;
以点A为圆心、AO长为半径的圆与y轴的交点,有1个;
以点O为圆心、OA长为半径的圆与y轴的交点,有2个.
以上四个点为所求.
| k1 |
| 3x |
| 1 |
| 3 |
∴k1=3×
| 1 |
| 3 |
∵反比例函数y=
| k1 |
| 3x |
∴a=1.
由直线y2=k2x+m过点A,B得:
|
解得
|
∴反比例函数关系式为y=-
| 1 |
| x |
(2)点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,-
| 2 |
| 2 |

如图,线段OA的垂直平分线与y轴的交点,有1个;
以点A为圆心、AO长为半径的圆与y轴的交点,有1个;
以点O为圆心、OA长为半径的圆与y轴的交点,有2个.
以上四个点为所求.
点评:此题综合考查了待定系数法求函数解析式的方法、等腰三角形的性质等知识,注意分类思想的运用.

练习册系列答案
相关题目
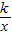 图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 .(只需写出符合条件的一个k的值)
图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 .(只需写出符合条件的一个k的值)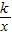 图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 .(只需写出符合条件的一个k的值)
图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 .(只需写出符合条件的一个k的值)