题目内容
(2013•达州)已知f(x)=
,则f(1)=
=
f(2)=
=
…,已知f(1)+f(2)+f(3)+…+f(n)=
,求n的值.
| 1 |
| x(x+1) |
| 1 |
| 1×(1+1) |
| 1 |
| 1×2 |
| 1 |
| 2×(2+1) |
| 1 |
| 2×3 |
| 14 |
| 15 |
分析:把f(x)裂项为
-
,然后进行计算即可得解.
| 1 |
| x |
| 1 |
| x+1 |
解答:解:∵f(x)=
=
-
,
∴f(1)+f(2)+f(3)+…+f(n)=1-
+
-
+
-
+…+
-
=1-
,
∵f(1)+f(2)+f(3)+…+f(n)=
,
∴1-
=
,
解得n=14.
| 1 |
| x(x+1) |
| 1 |
| x |
| 1 |
| x+1 |
∴f(1)+f(2)+f(3)+…+f(n)=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
∵f(1)+f(2)+f(3)+…+f(n)=
| 14 |
| 15 |
∴1-
| 1 |
| n+1 |
| 14 |
| 15 |
解得n=14.
点评:本题考查了分式的加减,把f(x)进行裂项是解题的关键,也是本题的难点.

练习册系列答案
相关题目
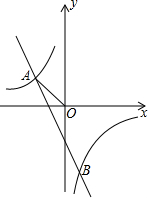 (2013•达州)已知反比例函数
(2013•达州)已知反比例函数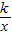 图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 .(只需写出符合条件的一个k的值)
图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 .(只需写出符合条件的一个k的值)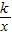 图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 .(只需写出符合条件的一个k的值)
图象上的点,当x1<x2<0时,y1<y2,则k的一个值可为 .(只需写出符合条件的一个k的值)