题目内容
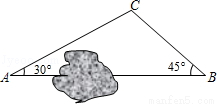
如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)

考点:
解直角三角形的应用.
分析:
过C作CD⊥AB于D,在Rt△ACD中,根据AC=10,∠A=30°,解直角三角形求出AD、CD的长度,然后在Rt△BCD中,求出BD、BC的长度,用AC+BC﹣(AD+BD)即可求解.
解答:
解:过C作CD⊥AB于D,
在Rt△ACD中,
∵AC=10,∠A=30°,
∴DC=ACsin30°=5,
AD=ACcos30°=5![]() ,
,
在Rt△BCD中,
∵∠B=45°,
∴BD=CD=5,BC=5![]() ,
,
则用AC+BC﹣(AD+BD)=10+5![]() ﹣(5
﹣(5![]() +5)=5+5
+5)=5+5![]() ﹣5
﹣5![]() (千米).
(千米).
答:汽车从A地到B地比原来少走(5+5![]() ﹣5
﹣5![]() )千米
)千米![]() .
.

点评:
本题考查了解直角三角形的应用,难度适中,解答本题的关键是作三角形的高建立直角三角形幷解直角三角形.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
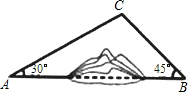 如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:
如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据: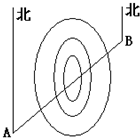 11、如图,A、B两地之间是一座山,现准备修一条隧道,在A地测得隧道北偏东51°,如果A、B两地同时开工,那么在B地应按
11、如图,A、B两地之间是一座山,现准备修一条隧道,在A地测得隧道北偏东51°,如果A、B两地同时开工,那么在B地应按 如图,A、B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,现开通隧道后,汽车直接沿直线AB行驶,已知AC=12km,BC=9km,∠A=30°,隧道开通后,汽车从A地到B地比原来少走多少路程?(结果保留整数) (参考数据:
如图,A、B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,现开通隧道后,汽车直接沿直线AB行驶,已知AC=12km,BC=9km,∠A=30°,隧道开通后,汽车从A地到B地比原来少走多少路程?(结果保留整数) (参考数据: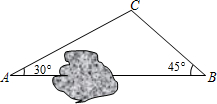 (2013•呼和浩特)如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)
(2013•呼和浩特)如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)