Question

【题目】探究发现

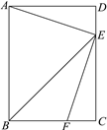
如图1，正方形中，点分别在上，．通过探究可以发现线段和之间存在一定的数量关系：

拓展延伸

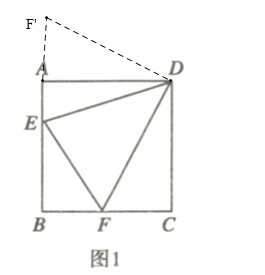
如图2，正方形中，点分别在的延长线上，

①线段和之间有怎样的数量关系?写出猜想，并加以证明；

②若，求的面积．

Answer 1

【答案】见详解；①见详解；②12．

【解析】

（1）把绕点D顺时针旋转，使DC与DA边重合，则，根据全等三角形的性质即可得出，再根据SAS即可证明，得出，最后根据线段的和与差及等量代换即可得证；

（2）①使绕D旋转，AE恰好落在CF上，构造出，根据全等三角形的性质即可得出，再根据SAS即可证明，得出，最后根据线段的和与差及等量代换即可得证；

②由①知，得出，根据正方形的性质即可得出,从而即可求出．

（1）把绕点D顺时针旋转，使DC与DA边重合，则

、A、E三点共线

在和中

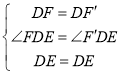
又

（2）①EF=CF-AE

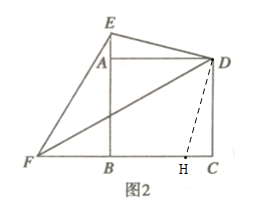
证明：使绕D旋转，AE恰好落在CF上，构造出

，DE=DH,AE=CH

在和中

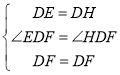
即EF=CF-AE

②由①知，

,EF=HF

四边形ABCD为正方形

,CD=AB=4

即