题目内容
如图①,△ABC中,AB=BC,∠B=90°,点A,B的坐标分别(0,10),(8,4),点C在 第一象限.动点P从点A出发沿边AB―BC匀速运动,同时动点Q以相同的速度在x轴上运动,图②是当点P在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象.
(1)求点P、Q运动的速度;
(2)求点C的坐标;
(3)求点P在边AB上运动时,△OPQ的面积S(平方单位)关于时间t(秒)的函数关系式,并求当点P运动到边AB上哪个位置时,△OPQ的面积最大?
(4)(本小题为选做题,做对另加3分,但全卷满分不超过150分)已知点P在边AB上运动时,∠OPQ的大小随时间t的增大而增大,点P在边BC上运动时,∠OPQ的大小随时间t的增大而减小,那么当点P在这两边上运动时,使∠OPQ =90°的点P有
______个(只填结论,不需解答过程).

图 ① 图②
解:(1)(11-1)÷10=1(长度单位/秒)
(2)如图,作CD⊥x轴于D,作EF∥x轴交y轴、CD分别于点E、F,
∵B(8,4)∴EB=8,OE=4,

∴AE=10-4=6,∴AB=BC=![]() ,∵∠ABC =90°
,∵∠ABC =90°
∴△BCF≌△ABE,∴BF=AE=6,CF=EB=8,∴CD=12,
OD=EF=EB+BF=14,∴C(14,12);
(3)作PG⊥y轴于G,则△AGP∽△AEB,∴![]() ,∴
,∴![]()
∴![]() ,
,![]() ,∴OG=10-
,∴OG=10-![]() ,由图②,当t=0时,x=1,∴OQ=1+t,
,由图②,当t=0时,x=1,∴OQ=1+t,
S△OPQ=![]()
∴![]() (
(![]() )
)
当![]() 时(在
时(在![]() 范围内),S最大.
范围内),S最大.
此时PG=![]() ,OG=10-
,OG=10-![]() ,∴P(
,∴P(![]() ).
).
(4)2

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案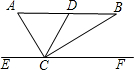 如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )
如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )| A、35° | B、45° | C、55° | D、65° |
 17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有:
17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有: 8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )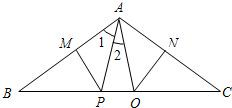 如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数.
如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数. 19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.
19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.