题目内容
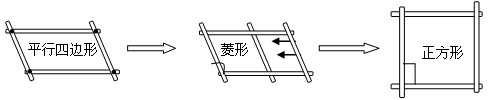
（2004•玉溪）观察下列图形的变化过程，解答以下问题：
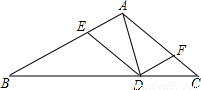
如图，在△ABC中，D为BC边上的一动点（D点不与B、C两点重合）．DE∥AC交AB于E点，DF∥AB交AC于F点．
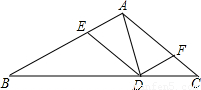
（1）试探索AD满足什么条件时，四边形AEDF为菱形，并说明理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF为正方形？为什么？
【答案】分析：（1）当AD平分∠BAC时，四边形AEDF为菱形．可先证明四边形AEDF为平行四边形，再证明一组邻边相等，即可证明四边形AEDF为菱形；
（2）当∠BAC=90°时，菱形AEDF是正方形．因为有一个角是直角的菱形是正方形．
解答：解：（1）当AD平分∠BAC时，四边形AEDF为菱形．
∵AE∥DF，DE∥AF，
∴四边形AEDF为平行四边形，
∵AD平分∠BAC，
∴∠EAD=∠FAD
又∠FAD=∠ADE，
∴∠DAE=∠ADE，
∴AE=DE，
∴平行四边形AEDF为菱形；
（2）当∠BAC=90°时，菱形AEDF是正方形．因为有一个角是直角的菱形是正方形．
点评：此题主要考查菱形和正方形的判定．
（2）当∠BAC=90°时，菱形AEDF是正方形．因为有一个角是直角的菱形是正方形．
解答：解：（1）当AD平分∠BAC时，四边形AEDF为菱形．
∵AE∥DF，DE∥AF，
∴四边形AEDF为平行四边形，
∵AD平分∠BAC，
∴∠EAD=∠FAD
又∠FAD=∠ADE，
∴∠DAE=∠ADE，
∴AE=DE，
∴平行四边形AEDF为菱形；
（2）当∠BAC=90°时，菱形AEDF是正方形．因为有一个角是直角的菱形是正方形．
点评：此题主要考查菱形和正方形的判定．
练习册系列答案
相关题目
（2004•玉溪）填表：
．
| 抛物线 | 对称轴 | 顶点坐标 | 图象的特征 |
| y=ax2 | x=0 | （0，0） | 对称轴为y轴，顶点在原点，a＞0时，开口向上，最低点是顶点；a＜0时，开口向下，最高点是顶点． |
| y=a（x+1）2-1 | x= | （-1，-1） | 形状与y=ax2相同，图象可由y=ax2的图象分别向 和 平移一个单位而得． |
（2004•玉溪）填表：
．
| 抛物线 | 对称轴 | 顶点坐标 | 图象的特征 |
| y=ax2 | x=0 | （0，0） | 对称轴为y轴，顶点在原点，a＞0时，开口向上，最低点是顶点；a＜0时，开口向下，最高点是顶点． |
| y=a（x+1）2-1 | x= | （-1，-1） | 形状与y=ax2相同，图象可由y=ax2的图象分别向 和 平移一个单位而得． |
（2004•石景山区模拟）观察下表中三角形个数变化规律，填表并回答下面问题．
问题：如果图中三角形的个数是102个，则图中应有 条横截线．
| 图形 |  |  |  |
| 横截线条数 | 1 | 2 | |
| 三角形个数 | 6 |