Question

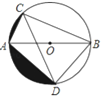
【题目】如图，AB为⊙O的直径，弦AC=2，∠ABC=30°，∠ACB的平分线交⊙O于点D，求：

（1）BC、AD的长；

（2）图中两阴影部分面积的和．

Answer 1

【答案】(1)2；（2）.

【解析】

（1）根据直径得出∠ACB=∠ADB=90°，根据勾股定理求出BC，根据圆周角定理求出AD=BD，求出AD即可；
（2）根据三角形的面积公式，求出△AOC和△AOD的面积，再求出S扇形COD，即可求出答案．

解：（1）∵AB是直径，

∴∠ACB=∠ADB=90°（直径所对的圆周角是直角），

在Rt△ABC中，∠ABC=30°，AC=2，

∴AB=4，

∴BC=，

∵∠ACB的平分线交⊙O于点D，

∴∠DCA=∠BCD

∴，

∴AD=BD，

∴在Rt△ABD中，AD=BD=AB=2；

（2）连接OC，OD，

∵∠ABC=30°，

∴∠AOC=∠2∠ABC=60°，

∵OA=OB，

∴S△AOC=S△ABC=××AC×BC=××2×2=，

由（1）得∠AOD=90°，

∴∠COD=150°，

S△AOD=×AO×OD=×22=2，

∴S阴影=S扇形COD﹣S△AOC﹣S△AOD=﹣﹣2=π﹣﹣2．