题目内容
18．计算：（1）（$\sqrt{6}$+$\sqrt{10}$×$\sqrt{15}$）×$\sqrt{3}$．
（2）已知a=-2-$\sqrt{3}$，b=$\sqrt{3}$-2，求（a+b）2+（a-b）（2a+b）-3a2值．
分析 （1）利用二次根式的乘法法则运算；
（2）先利用乘法公式展开，再合并得到原式=ab，然后把a、b的值代入后利用平方差公式计算．
解答 解：（1）原式=$\sqrt{6×3}$+$\sqrt{10×15×3}$
=3$\sqrt{2}$+15$\sqrt{2}$
=18$\sqrt{2}$；
（2）原式=a2+2ab+b2+2a2+ab-2ab-b2-3a2
=ab，
当a=-2-$\sqrt{3}$，b=$\sqrt{3}$-2，原式=（-2-$\sqrt{3}$）（$\sqrt{3}$-2）=-（$\sqrt{3}$+2）（$\sqrt{3}$-2）=-（3-4）=1．
点评 本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．（1）图（1）是正方体木块，把它切去一块，可能得到形如图（2），（3），（4），（5）的木块．
我们知道，图（1）的正方体木块有8个顶点，12条棱，6个面，请你将图（2），（3），（4），（5）中木块的顶点数，棱数，面数填入表：
（2）观察表，请你归纳上述各种木块的顶点数，棱数，面数之间的数量关系，这种数量关系是：
顶点数+面数-2=棱数．
（3）图⑥是用虚线画出的正方体木块，请你想象一种与图②～⑤不同的切法，把切去一块后得到的那一块的每条棱都改画成实线，则该木块的顶点数为8，棱数为12，面数为6．这与你（2）题中所归纳的关系是否相符？
我们知道，图（1）的正方体木块有8个顶点，12条棱，6个面，请你将图（2），（3），（4），（5）中木块的顶点数，棱数，面数填入表：
| 图 | 顶点数 | 棱数 | 面数 |
| （1） | 8 | 12 | 6 |
| （2） | 6 | 9 | 5 |
| （3） | 8 | 12 | 6 |
| （4） | 8 | 13 | 7 |
| （5） | 10 | 15 | 7 |
顶点数+面数-2=棱数．
（3）图⑥是用虚线画出的正方体木块，请你想象一种与图②～⑤不同的切法，把切去一块后得到的那一块的每条棱都改画成实线，则该木块的顶点数为8，棱数为12，面数为6．这与你（2）题中所归纳的关系是否相符？
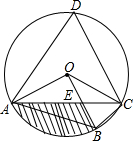如图，四边形ABCD是⊙O的内接四边形，∠ABC=2∠D，连结OA、OB、OC、AC，OB与AC相交于点E．
3．下列图形中不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，P为矩形ABCD边上的一个动点，沿ABCD方向运动，P点运动的路程为x．△PAD的面积为y，则y与x的函数关系用图象表示大致是（ ）
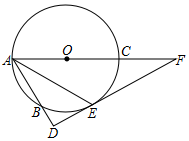如图，AC为⊙O的直径，DAB为⊙O的割线，E为⊙O上一点，弧BE=弧CE，DE⊥AB于D，交AO的延长线于F