Question

【题目】如图，给出五个等量关系：①AD＝BC；②AC＝BD；③CE＝DE；④∠D＝∠C；⑤∠DAB＝∠CBA．

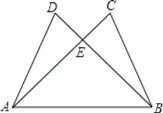
请你以其中两个为条件，另外三个中的一个为结论，推出一个正确的结论（只需写出一种情况），并加以证明．

已知：

求证：

证明：

Answer 1

【答案】见解析.

【解析】

选择由①②推出③④⑤，理由是根据SSS证△DAB≌△CBA，推出④⑤，根据AAS证△DAE≌△CBE，能推出③．

已知AD=BC，AC=BD，
求证CE=DE，∠D=∠C，∠DAB=∠CBA，
证明：在△DAB和△CBA中

∴△DAB≌△CBA（SSS），
∴∠D=∠C，∠DAB=∠CBA，
在△DAE和△CBE中

∴△DAE≌△CBE（AAS），
∴CE=DE，
即由条件①②能推出结论③，或④，或⑤．