题目内容
4.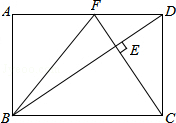 在矩形ABCD中,CF⊥BD分别交BD、AD于点E、F,连接BF,若点F为AD的中点,则$\frac{AB}{BC}$=( )
在矩形ABCD中,CF⊥BD分别交BD、AD于点E、F,连接BF,若点F为AD的中点,则$\frac{AB}{BC}$=( )| A. | 1:$\sqrt{3}$ | B. | 2:$\sqrt{3}$ | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:$\sqrt{3}$ |
分析 根据F为AD的中点,可得FB=FC,根据AD∥BC,可得FE:EC=FD:BC=1:2,设EF=x,则EC=2x,FC=3x,利用射影定理求出DF=$\sqrt{3}$x,DC=$\sqrt{6}$x,继而得出BC=AD=2DF=2$\sqrt{3}$x,AB=DC=$\sqrt{6}$x,即可求得$\frac{AB}{BC}$的值.
解答 解:∵F为AD的中点,AD∥BC,
∴FE:EC=FD:BC=1:2,
设EF=x,则EC=2x,FC=3x,
∵CF⊥BD,
∴DF2=EF•CF=x•3x=3x2,DC2=CE•FC=2x•3x=6x2,
∴DF=$\sqrt{3}$x,DC=$\sqrt{6}$x,
∴BC=AD=2DF=2$\sqrt{3}$x,AB=DC=$\sqrt{6}$x,
∴$\frac{AB}{BC}$=$\frac{\sqrt{6}x}{2\sqrt{3}x}$=$\frac{\sqrt{2}}{2}$.
故选C.
点评 本题考查了矩形的性质,平行线分线段成比例定理,射影定理,解答本题的关键是根据射影定理得出BC和AB的值.

练习册系列答案
相关题目
19.甲、乙两名同学本学期参加的11次考试成绩(单位:分)如下表所示:
(1)求两人的平均分及方差;
(2)分析他们的成绩各有什么特点;
(3)现要从两人中选一人参加比赛,历届比赛成绩表明,平均成绩达98分以上(含98分)才可能迸人决赛,你认为应该选谁参加这次比赛呢?为什么?
| 甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
| 乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
(2)分析他们的成绩各有什么特点;
(3)现要从两人中选一人参加比赛,历届比赛成绩表明,平均成绩达98分以上(含98分)才可能迸人决赛,你认为应该选谁参加这次比赛呢?为什么?
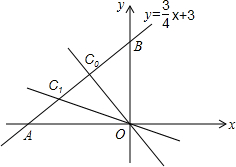 一次函数y=$\frac{3}{4}$x+m的图象过点(4,6),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动.
一次函数y=$\frac{3}{4}$x+m的图象过点(4,6),且分别与x轴、y轴交于A、B点,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴正半轴上运动.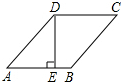 如图,在菱形ABCD中.DE⊥AB于E,DE=2,∠C=45°,则BE长是2$\sqrt{2}$-2.
如图,在菱形ABCD中.DE⊥AB于E,DE=2,∠C=45°,则BE长是2$\sqrt{2}$-2.