题目内容
7.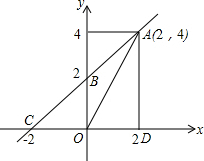 如图一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,求直线AB的一次函数解析式及△AOC的面积.
如图一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,求直线AB的一次函数解析式及△AOC的面积.
分析 (1)根据待定系数法即可求得;
(2)根据三角形面积公式即可求得.
解答 解:∵一次函数y=kx+b经过点A(2,4)和B(0,2)两点;
∴$\left\{{\begin{array}{l}{4=2k+b}\\{2=b}\end{array}}\right.$
∴$\left\{{\begin{array}{l}{k=1}\\{b=2}\end{array}}\right.$
∴所求一次函数为y=x+2,
∵点C(-2,0)
∴OC=2;
∴${S_{△AOC}}=\frac{1}{2}•OC•|{y_A}|=\frac{1}{2}×2×4=4$.
点评 本题考查了待定系数法求一次函数的解析式,三角形的面积,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
15.在△ABC中,∠C=90°,AB的垂直平分线DE交AB于E,交BC于D,且CD:BD=1:2,BC=6cm,则D到AB的距离为多少( )
| A. | 1.5cm | B. | 2cm | C. | 3cm | D. | 4cm |
12.如果10b=n,那么称b为n的劳格数,记为b=d (n),由定义可知:10b=n与b=d (n)所表示的是b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)=1,d(10-2)=-2;
劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数).
(2)下表中与数x对应的劳格数d (x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
(1)根据劳格数的定义,填空:d(10)=1,d(10-2)=-2;
劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数).
(2)下表中与数x对应的劳格数d (x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d(x) | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
19.下列调查适合作抽样调查的是( )
| A. | 了解巫溪网“今日巫溪”栏目的阅览率 | |
| B. | 了解某甲型H1N1确诊病人同机乘客的健康状况 | |
| C. | 了解某班每个学生家庭电脑的数量 | |
| D. | 对“歼20”隐形战斗机零部件的检查 |
16.用配方法解方程x2+4x-5=0,下列配方正确的是( )
| A. | (x+2)2=1 | B. | (x+2)2=5 | C. | (x+2)2=9 | D. | (x+4)2=9 |

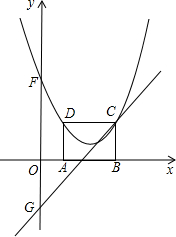 如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2,直线y=x-2经过点C,交y轴于点G.
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2,直线y=x-2经过点C,交y轴于点G.