题目内容
小明同学在东西方向的沿江大道A处,测得江中灯塔P在北偏东60°方向上,在A处正东400米的B处,测得江中灯塔P在北偏东30°方向上,则灯塔P到沿江大道的距离为 米.
【答案】分析:过点P作PD⊥AB于点D,根据已知可得△ABP是等腰三角形,再根据三角函数定义即可求得PD的长.
解答: 解:由已知得,∠A=30°,∠ABP=120°,
解:由已知得,∠A=30°,∠ABP=120°,
∴∠APB=30°.
∴AB=BP=400.
过点P作PD⊥AB于点D.
在直角△PBD中,∠PBD=60°,
∴PD=PB•sin60°=200 (米).
(米).
点评:本题主要考查了方向角含义,正确记忆三角函数的定义是解决本题的关键.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
解答:
 解:由已知得,∠A=30°,∠ABP=120°,
解:由已知得,∠A=30°,∠ABP=120°,∴∠APB=30°.
∴AB=BP=400.
过点P作PD⊥AB于点D.
在直角△PBD中,∠PBD=60°,
∴PD=PB•sin60°=200
 (米).
(米).点评:本题主要考查了方向角含义,正确记忆三角函数的定义是解决本题的关键.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
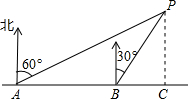 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.| A、250 | ||
| B、500 | ||
C、250
| ||
D、500
|
 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC= 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC等于多少米?
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC等于多少米?