题目内容
在直角坐标系xOy中,已知某二次函数的图象经过A(-4,0)、B(0,-3),与x轴的正半轴相交于点C,若△AOB∽△BOC(相似比不为1).
1.(1)求这个二次函数的解析式;
2.(2)求△ABC的外接圆半径r;
3.(3)在线段AC上是否存在点M(m,0),使得以线段BM为直径的圆与线段AB交于N点,且以点O、A、N为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
1.⑴∵△AOB∽△BOC(相似比不为1),
∴![]() . 又∵OA=4,OB=3,
. 又∵OA=4,OB=3,
∴OC=32×![]() =
=![]() .∴点C(
.∴点C(![]() ,0). …………………1分
,0). …………………1分
设图象经过A、B、C三点的函数解析式是y=ax2+bx+c,
 则c= -3,且
则c= -3,且 …………………2分
…………………2分
即![]()
解得,a=![]() , b=
, b= .
.
∴这个函数的解析式是y = x2+
x2+![]() x-3.
x-3.
2.⑵∵△AOB∽△BOC(相似比不为1),
∴∠BAO=∠CBO.
又∵∠ABO+ ∠BAO =90°,
∴∠ABC=∠ABO+∠CBO=∠ABO+∠BAO=90°. ………………4分
∴AC是△ABC外接圆的直径.
∴ r =![]() AC=
AC=![]() ×[
×[![]() -(-4)]=
-(-4)]=![]() .
.
3.⑶∵点N在以BM为直径的圆上,
∴ ∠MNB=90°. ……………………6分
①.当AN=ON时,点N在OA的中垂线上,
∴点N1是AB的中点,M1是AC的中点.
∴AM1= r=![]() ,点M1(-
,点M1(-![]() , 0),即m1=-
, 0),即m1=-![]() . ………………7分
. ………………7分
②. 当AN=OA时,Rt△AM2N2≌Rt△ABO,
∴AM2=AB=5,点M2(1, 0),即m2=1.
③. 当ON=OA时,点N显然不能在线段AB上.
综上,符合题意的点M(m,0)存在,有两解:
m= -![]() ,或1.
,或1.
解析:略

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
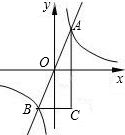 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.