题目内容
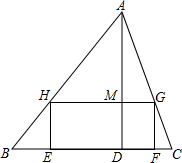 如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
(1)设矩形EFGH的长HG=y,宽HE=x,确定y与x的函数关系式;(提示:S△ABC=S△AHG+S梯形BCGH)
(2)设矩形EFGH的面积为S,确定S与x的函数关系式;
(3)当x为何值时,矩形EFGH的面积S最大?
解:(1)∵S△ABC=S△AHG+S梯形BCGH,
∴ ×160×120=
×160×120= y(120-x)+
y(120-x)+ x(y+160),
x(y+160),
化简得:y=- x+160;
x+160;
(2)把y=- x+160代入S=xy,
x+160代入S=xy,
得:S=- x2+160x;
x2+160x;
(3)将S=- x2+160x,
x2+160x,
右边配方得:S=- (x-60)2+4800;
(x-60)2+4800;
∵- (x-60)2≤0,
(x-60)2≤0,
∴当- (x-60)2=0时,即x=60时,S=-
(x-60)2=0时,即x=60时,S=- (x-60)2+4800有最大值4800.
(x-60)2+4800有最大值4800.
分析:(1)由S△ABC=S△AHG+S梯形BCGH,可得 ×160×120=
×160×120= y(120-x)+
y(120-x)+ x(y+160),继而求得答案;
x(y+160),继而求得答案;
(2)把y=- x+160代入S=xy,即可求得S与x的函数关系式;
x+160代入S=xy,即可求得S与x的函数关系式;
(3)由S=- x2+160x,可得:S=-
x2+160x,可得:S=- (x-60)2+4800;则可求得矩形EFGH的面积S最大值.
(x-60)2+4800;则可求得矩形EFGH的面积S最大值.
点评:此题考查了相似三角形的判定与性质以及二次函数的性质.此题难度适中,注意掌握方程思想与数形结合思想的应用.
∴
 ×160×120=
×160×120= y(120-x)+
y(120-x)+ x(y+160),
x(y+160),化简得:y=-
 x+160;
x+160;(2)把y=-
 x+160代入S=xy,
x+160代入S=xy,得:S=-
 x2+160x;
x2+160x;(3)将S=-
 x2+160x,
x2+160x,右边配方得:S=-
 (x-60)2+4800;
(x-60)2+4800;∵-
 (x-60)2≤0,
(x-60)2≤0,∴当-
 (x-60)2=0时,即x=60时,S=-
(x-60)2=0时,即x=60时,S=- (x-60)2+4800有最大值4800.
(x-60)2+4800有最大值4800.分析:(1)由S△ABC=S△AHG+S梯形BCGH,可得
 ×160×120=
×160×120= y(120-x)+
y(120-x)+ x(y+160),继而求得答案;
x(y+160),继而求得答案;(2)把y=-
 x+160代入S=xy,即可求得S与x的函数关系式;
x+160代入S=xy,即可求得S与x的函数关系式;(3)由S=-
 x2+160x,可得:S=-
x2+160x,可得:S=- (x-60)2+4800;则可求得矩形EFGH的面积S最大值.
(x-60)2+4800;则可求得矩形EFGH的面积S最大值.点评:此题考查了相似三角形的判定与性质以及二次函数的性质.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
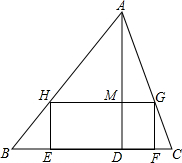 如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M. 在底边长BC=20cm,高AM=12cm的三角形铁板ABC上,要截一块矩形铁板EFGH,如图所示,当矩形的边EF=
在底边长BC=20cm,高AM=12cm的三角形铁板ABC上,要截一块矩形铁板EFGH,如图所示,当矩形的边EF= 所在圆的圆心O(
所在圆的圆心O( 保留作图痕迹,不写作法);
保留作图痕迹,不写作法); 
