Question

2．如图①，在平面直角坐标系中，点A的坐标为（1，2），点B的坐标为（4，5），二次函数y=x²的图象记为抛物线l₁．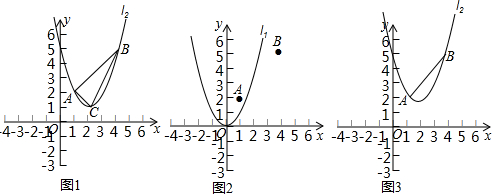

（1）平移抛物线l₁，使平移后的抛物线过A，B两点，记为抛物线l₂，如图②，求抛物线l₂的函数表达式；
（2）请在图②上用尺规作图的方式探究抛物线l₂上是否存在点P，使△ABP为等腰三角形？若存在，请判断点P共有几个可能的位置（保留作图痕迹）并在图中画出P点，以P₁、P₂、P₃、表示不同的点；若不存在，请说明理由．
（3）设抛物线l₂的顶点为C，K为抛物线l₂一点．若S_△ABK=S_△ABC，求点K的坐标．

Answer 1

分析 （1）根据待定系数法，可得函数解析式；
（2）根据等腰三角形的定义：P₁A=P₁B，P₂A=P₂B，P₃B=AB，P₅B=P₂B，P₄A=P₂A，可得答案；
（3）根据平行线的间距离相等，可得AB的平行线CK₁，K₂K₃，根据解方程组，可得自变量，根据自变量与函数值的对应关系，可得答案．

解答 解：（1）设抛物线的解析式为y=x²=bx+c．将点A、B的坐标代入得$\left\{\begin{array}{l}{1+b+c=2}\\{16+4b+c=5}\end{array}\right.$．
解得：$\left\{\begin{array}{l}{b=-4}\\{c=5}\end{array}\right.$．
抛物线的解析式为y=x²-4x+5．
（2）如图1：，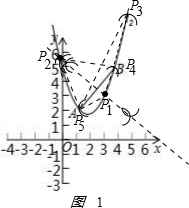
P₁A=P₁B，P₂A=P₂B，P₃B=AB，P₅B=P₂B，P₄A=P₂A； 
（3）如图2：，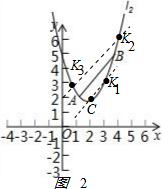
y=x²-4x+5=（x-2）²+1，顶点C的坐标为（2，1）．
AB的解析式为y=x+1，设过C点平行于AB的直线为y=x+b，
将C（2，1）代入函数解析式，得
2+b=1，解得b=-1，
过C点平行于AB的直线为y=x-1，
联立CK₁与抛物线，得
$\left\{\begin{array}{l}{y=x-1}\\{y={x}^{2}-4x+5}\end{array}\right.$，
消元化简，得
x²-5x+6=0，解得x=2（不符合题意，舍），x=3，
当x=3时，y=x-1=2，即K₁（3，2）；
设平行于AB且到AB的距离等于CK₁到AB的距离K₂K₃，
AB向下平移两个单位得CK₁，AB向上平移两个单位得K₂K₃
K₂K₃的解析式为y=x+1+2，即y=x+3，
联立K₂K₃与抛物线，得
$\left\{\begin{array}{l}{y=x+3}\\{y={x}^{2}-4x+5}\end{array}\right.$，
消元化简，得
x²-5x+2=0，解得x=$\frac{5+\sqrt{17}}{2}$，x=$\frac{5-\sqrt{17}}{2}$，
当x=$\frac{5+\sqrt{17}}{2}$时，y=x+3=$\frac{11+\sqrt{17}}{2}$，即K₂（$\frac{5+\sqrt{17}}{2}$，$\frac{11+\sqrt{17}}{2}$）；
当x=$\frac{5-\sqrt{17}}{2}$时，y=x+3=$\frac{11-\sqrt{17}}{2}$，即K₂（$\frac{5+\sqrt{17}}{2}$，$\frac{11+\sqrt{17}}{2}$）；
综上所述：若S_△ABK=S_△ABC，点K的坐标K₁（3，2），K₂（$\frac{5+\sqrt{17}}{2}$，$\frac{11+\sqrt{17}}{2}$），K₂（$\frac{5+\sqrt{17}}{2}$，$\frac{11+\sqrt{17}}{2}$）．

点评 本题考查了二次函数综合题，利用等腰三角形的定义得出P₁A=P₁B，P₂A=P₂B，P₃B=AB，P₅B=P₂B，P₄A=P₂A是解题关键；利用平行线的间距离相等得出AB的平行线CK₁，K₂K₃是解题关键．