Question

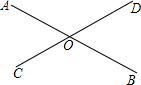如图，AB和CD交于点O，则∠AOC的邻补角是

∠AOD和∠BOC

．∠AOC的对顶角是

∠BOD

，若∠AOC=40°，则∠BOD=

40°

，∠AOD=

140°

，∠BOC=

140°

．

Answer 1

分析：根据邻补角的定义以及对顶角的定义解答即可；
先根据对顶角相等可得∠BOD=∠AOC，再根据邻补角的定义解答．

解答：解：AB和CD交于点O，则∠AOC的邻补角是∠AOD和∠BOC；
∠AOC的对顶角是∠BOD，
∵∠AOC=40°，
∴∠BOD=∠AOC=40°，
∠AOD=180°-∠AOC=180°-40°=140°，
∠BOC=∠AOD=140°．
故答案为：∠AOD和∠BOC；∠BOD；40°；140°；140°．

点评：本题考查了对顶角、邻补角的定义，熟记概念与性质并准确识图是解题的关键．