题目内容
【题目】如图,在△ABC中、D、E分别是AB,BC上任意一点,连结DE,若BD=4,DE=5.
(1)BE的取值范围 ;
(2)若DE∥AC,∠A=85°,∠BED=35°,求∠B的度数.
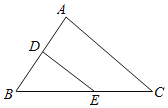
【答案】(1)1<BE<9;(2)60°.
【解析】
(1)根据三角形的三边关系即可得出结论;
(2)根据平行线的性质,即可得到∠BED=∠C=35°,然后根据三角形的内角和定理即可求出∠B的度数.
解:(1)∵BD=4,DE=5,
∴△BDE中,5﹣4<BE<5+4,
即1<BE<9,
即BE的取值范围为:1<BE<9;
故答案为:1<BE<9;
(2)∵DE∥AC,
∴∠BED=∠C=35°,
又∵∠A=85°,
∴△ABC中,∠B=180°﹣∠A﹣∠C=180°﹣85°﹣35°=60°.

练习册系列答案
相关题目