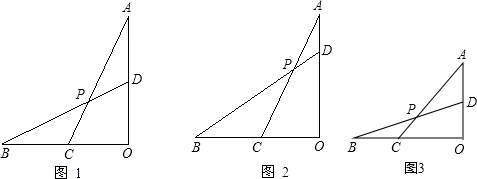
题目内容
已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.
(1)如图1,当OA=OB,且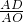 =
= 时,求
时,求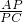 的值;
的值;
(2)如图2,当OA=OB,且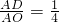 时,①
时,①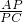 =______;②证明:∠BPC=∠A;
=______;②证明:∠BPC=∠A;
(3)如图3,当AD:AO:OB=1:n: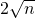 时,直接写出tan∠BPC的值.
时,直接写出tan∠BPC的值.

 解:(1)过C作CE∥BD交AO于点E,如图,
解:(1)过C作CE∥BD交AO于点E,如图,∵点C为OB中点,
∴CE为△OBD的中位线,
∴DE=OE,
∵PD∥CE,
∴
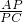 =
= ,
,又∵
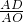 =
= ,
,∴AD=DO,
∴AD=2DE,
∴
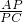 =2;
=2;(2)①过C作CE∥BD交AO于点E,如图,
∵点C为OB中点,
∴CE为△OBD的中位线,
∴DE=OE,
∵PD∥CE,
∴
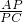 =
= ,
,又∵
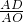 =
= ,
,∴DO=3AD,
∴2DE=3AD,
∴AD=
 DE,
DE,∴
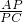 =
= ;
;②设OB=8a,
∴OA=OB=8a,OC=4a,
AD=2a,DE=OE=3a,
而OA⊥OB,
∴∠COE=90°,
在Rt△OCE中,OC=4a,OE=3a,则CE=
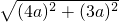 =5a,
=5a,∴EC=EA,
∴∠ACE=∠A,
而CE∥BD,
∴∠BPC=∠ACE,
∴∠BPC=∠A;
故答案为
 ;
;(3)过D作DF⊥AC,垂足为F,过C作CE∥BD交AO于点E,如图,
设AD=a,则AO=na,OB=2a
 ,
,∵点C为OB中点,
∴CO=a
 ,
,在Rt△ACO中,AC=
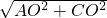 =
=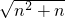 a,
a,又∵Rt△ADF∽Rt△ACO,
∴AF:AO=DF:OC=AD:AC,即AF:na=DF:
 a=a:
a=a: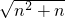 a,
a,∴AF=
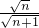 a,DF=
a,DF=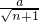 ,
,又∵PD∥CE,
∴AP:AC=AD:AE,即AP:
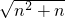 a=a:
a=a: a,
a,∴AP=
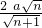 ,
,∴PF=AP-AF=
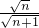 a,
a,∴tan∠FPD=
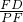 =
=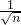 =
=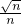 .
.∴tan∠BPC=
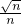 .
.分析:(1)过C作CE∥BD交AO于点E,则CE为△OBD的中位线,得到DE=OE,由PD∥CE,根据平行线分线段成比例定理得
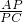 =
= ,又
,又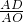 =
= 得AD=DO,则有AD=2DE,即可得到
得AD=DO,则有AD=2DE,即可得到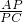 =2;
=2;(2)①与(1)不同的是
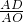 =
= 则DO=3AD,得2DE=3AD即AD=
则DO=3AD,得2DE=3AD即AD= DE,则
DE,则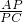 =
= ;②设OB=8a,则OA=OB=8a,OC=4a,AD=2a,DE=OE=3a,根据勾股定理得到CE=
;②设OB=8a,则OA=OB=8a,OC=4a,AD=2a,DE=OE=3a,根据勾股定理得到CE=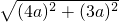 =5a,则有EC=EA,得到∠ACE=∠A,而∠BPC=∠ACE,即可得到结论;
=5a,则有EC=EA,得到∠ACE=∠A,而∠BPC=∠ACE,即可得到结论;(3)过D作DF⊥AC,垂足为F,过C作CE∥BD交AO于点E,设AD=a,则AO=na,OB=2a
 ,由点C为OB中点,则CO=a
,由点C为OB中点,则CO=a ,利用勾股定理可计算得AC=
,利用勾股定理可计算得AC=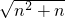 a,易证得Rt△ADF∽Rt△ACO,得到AF:AO=DF:OC=AD:AC,即AF:na=DF:
a,易证得Rt△ADF∽Rt△ACO,得到AF:AO=DF:OC=AD:AC,即AF:na=DF: a=a:
a=a: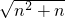 a,求出AF=
a,求出AF=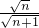 a,DF=
a,DF=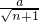 ,再根据平行线分线段成比例定理得到AP:AC=AD:AE,即AP:
,再根据平行线分线段成比例定理得到AP:AC=AD:AE,即AP: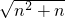 a=a:
a=a: a,求出AP=
a,求出AP=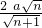 ,则PF=AP-AF=
,则PF=AP-AF=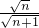 a,然后根据正切的定义即可得到tan∠FPD,从而得到tan∠BPC的值.
a,然后根据正切的定义即可得到tan∠FPD,从而得到tan∠BPC的值.点评:本题考查了平行线分线段成比例定理:如果一组平行线被两条直线所截,那么所截得的线段对应成比例.也考查了三角形中位线的性质、勾股定理以及锐角三角函数的定义.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目

 的值;
的值; 时,求tan∠BPC的值.
时,求tan∠BPC的值. 时,直接写出tan∠BPC的值.
时,直接写出tan∠BPC的值.
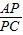 的值;
的值; 时,求tan∠BPC的值.
时,求tan∠BPC的值. 时,直接写出tan∠BPC的值.
时,直接写出tan∠BPC的值.