题目内容
已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.(1)如图1,当OA=OB,且D为OA中点时,求
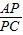 的值;
的值;(2)如图2,当OA=OB,且
 时,求tan∠BPC的值.
时,求tan∠BPC的值.(3)如图3,当AD:AO:OB=1:n:
 时,直接写出tan∠BPC的值.
时,直接写出tan∠BPC的值.
【答案】分析:(1)过D作BO的平行线,根据平行线分线段成比例定理,在△ACO中ED:CO=AD:AO,在△PDE和△PCB中,ED:BC=PE:PC,再根据C是BO的中点,可以求出PE:PC=1:2,再根据三角形中位线定理,点E是AC的中点,利用比例变形即可求出AP与PC的比值等于2;
(2)同(1)的方法,先求出PC= AC,再过D作DF⊥AC于F,设AD为a,利用勾股定理求出AC等于2
AC,再过D作DF⊥AC于F,设AD为a,利用勾股定理求出AC等于2 a,再利用相似三角形对应边成比例求出DF、AF的值,而PF=AC-AF-PC,也可求出,又∠BPC与∠FPD是对顶角,所以其正切值便可求出.
a,再利用相似三角形对应边成比例求出DF、AF的值,而PF=AC-AF-PC,也可求出,又∠BPC与∠FPD是对顶角,所以其正切值便可求出.
(3)根据(2)的方法,把相应数据进行代换即可求出.
解答:
解:(1)过D作DE∥CO交AC于E,
∵D为OA中点,
∴AE=CE= ,
, ,
,
∵点C为OB中点,
∴BC=CO, ,
,
∴ ,
,
∴PC= =
= ,
,
∴ =2;
=2;
(2)过点D作DE∥BO交AC于E,
∵ ,
,
∴ =
= =
= ,
,
∵点C为OB中点,
∴ ,
,
∴ ,
,
∴PC= =
= ,
,
过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,
∵OA=OB,点C为OB中点,
∴CO=2a,
在Rt△ACO中,AC= =
= =2
=2 a,
a,
又∵Rt△ADF∽Rt△ACO,
∴ ,
,
∴AF= ,DF=
,DF= ,
,
PF=AC-AF-PC=2 a-
a- -
- =
= ,
,
tan∠BPC=tan∠FPD= =
= .
.
(3)与(2)的方法相同,设AD=a,求出DF= a,
a,
PF= a,所以tan∠BPC=
a,所以tan∠BPC= .
.
点评:本题难度较大,需要对平行线分线段成比例定理灵活运用,根据勾股定理构造出直角三角形并求出其直角边的长,准确作出辅助线是解决本题的关键,也是求解的难点,这就要求同学们在平时的学习中对公式定理要熟练掌握并灵活运用,不断提高自己的数学学习能力.
(2)同(1)的方法,先求出PC=
 AC,再过D作DF⊥AC于F,设AD为a,利用勾股定理求出AC等于2
AC,再过D作DF⊥AC于F,设AD为a,利用勾股定理求出AC等于2 a,再利用相似三角形对应边成比例求出DF、AF的值,而PF=AC-AF-PC,也可求出,又∠BPC与∠FPD是对顶角,所以其正切值便可求出.
a,再利用相似三角形对应边成比例求出DF、AF的值,而PF=AC-AF-PC,也可求出,又∠BPC与∠FPD是对顶角,所以其正切值便可求出.(3)根据(2)的方法,把相应数据进行代换即可求出.
解答:

解:(1)过D作DE∥CO交AC于E,
∵D为OA中点,
∴AE=CE=
 ,
, ,
,∵点C为OB中点,
∴BC=CO,
 ,
,∴
 ,
,∴PC=
 =
= ,
,∴
 =2;
=2;(2)过点D作DE∥BO交AC于E,
∵
 ,
,∴
 =
= =
= ,
,∵点C为OB中点,
∴
 ,
,∴
 ,
,∴PC=
 =
= ,
,过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,
∵OA=OB,点C为OB中点,
∴CO=2a,
在Rt△ACO中,AC=
 =
= =2
=2 a,
a,又∵Rt△ADF∽Rt△ACO,
∴
 ,
,∴AF=
 ,DF=
,DF= ,
,PF=AC-AF-PC=2
 a-
a- -
- =
= ,
,tan∠BPC=tan∠FPD=
 =
= .
.(3)与(2)的方法相同,设AD=a,求出DF=
 a,
a,PF=
 a,所以tan∠BPC=
a,所以tan∠BPC= .
.点评:本题难度较大,需要对平行线分线段成比例定理灵活运用,根据勾股定理构造出直角三角形并求出其直角边的长,准确作出辅助线是解决本题的关键,也是求解的难点,这就要求同学们在平时的学习中对公式定理要熟练掌握并灵活运用,不断提高自己的数学学习能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
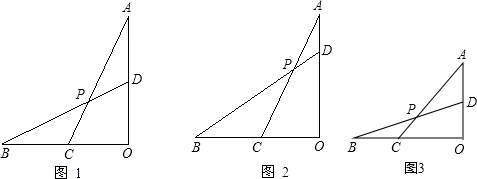

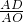 =
= 时,求
时,求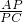 的值;
的值;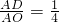 时,①
时,①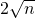 时,直接写出tan∠BPC的值.
时,直接写出tan∠BPC的值.
 的值;
的值; 时,求tan∠BPC的值.
时,求tan∠BPC的值. 时,直接写出tan∠BPC的值.
时,直接写出tan∠BPC的值.