Question

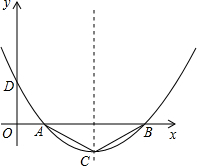
如图，二次函数y=ax²+bx+c的图象的顶点C的坐标为（0，-2），交x轴于A、B两点，其中A（-1，0），直线l：x=m（m＞1）与x轴交于D。

（1）求二次函数的解析式和B的坐标；

（2）在直线l上找点P（P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求点P的坐标（用含m的代数式表示）；

（3）在（2）成立的条件下，在抛物线上是否存在第一象限内的点Q，使△BPQ是以P为直角顶点的等腰直角三角形？如果存在，请求出点Q的坐标；如果不存在，请说明理由。

Answer 1

解：（1）①二次函数y=ax²+bx+c图象的顶点C的坐标为（0，-2），c = -2 ,  - , b=0 ,

点A(-1,0)、点B是二次函数y=ax²-2 的图象与x轴的交点，a-2=0,a=2. 二次函数的解析式为y=2x²-2；

②点B与点A(-1,0)关于直线x=0对称，点B的坐标为（1，0）；

（2）∠BOC=∠PDB=90º，点P在直线x=m上，

设点P的坐标为（m,p）, OB=1， OC=2， DB= m-1 , DP=|p| ，

①当△BOC∽△PDB时，,,p= 或p = ,

点P的坐标为（m，）或（m，）；

②当△BOC∽△BDP时， ，，p=2m-2或p=2-2m,

点P的坐标为（m，2m-2）或（m，2-2m）；

综上所述点P的坐标为（m，）、（m，）、（m，2m-2）或（m，2-2m）；

（3）不存在满足条件的点Q。

点Q在第一象限内的抛物线y=2x²-2上，

令点Q的坐标为（x, 2x²-2），x>1, 过点Q作QE⊥直线l ,

垂足为E，△BPQ为等腰直角三角形，PB=PQ，∠PEQ=∠PDB，

∠EPQ=∠DBP，△PEQ≌△BDP，QE=PD，PE=BD，

①     当P的坐标为（m，）时，

m-x = ，              m=0            m=1

 2x²-2- = m-1,        x=           x=1

与x>1矛盾,此时点Q不满足题设条件；

②     当P的坐标为（m，）时，

x-m=                      m=-           m=1

2x²-2- = m-1,            x=-           x=1

与x>1矛盾,此时点Q不满足题设条件；

③     当P的坐标为（m，2m-2）时，

m-x =2m-2                 m=          m=1

2x²-2-(2m-2) = m-1,        x=-         x=1

与x>1矛盾,此时点Q不满足题设条件；

④当P的坐标为（m，2-2m）时，

x- m = 2m-2           m=            m=1

2x²-2-(2-2m) = m-1     x=-            x=1

与x>1矛盾,此时点Q不满足题设条件；

综上所述，不存在满足条件的点Q。