题目内容
7．正三边形的边长为10，则它的半径为$\frac{10\sqrt{3}}{3}$，边心距为$\frac{5\sqrt{3}}{3}$．分析 过点O作OD⊥BC于点D，根据OB=OC可得出BD=CD=$\frac{1}{2}$BC=5，根据正三角形的性质得出∠BOC的度数，故可得出∠DOC度数，由直角三角形的性质即可得出OC及OD的长．
解答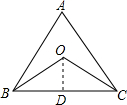 
解：如图所示，过点O作OD⊥BC于点D，
∵OB=OC，
∴BD=CD=$\frac{1}{2}$BC=5．
∵∠BOC=$\frac{360°}{3}$=120°，
∴∠DOC=60°，
∴OC=$\frac{CD}{sin60°}$=$\frac{5}{\frac{\sqrt{3}}{2}}$=$\frac{10\sqrt{3}}{3}$，OD=$\frac{CD}{tan60°}$=$\frac{5}{\sqrt{3}}$=$\frac{5\sqrt{3}}{3}$．
故答案为：$\frac{10\sqrt{3}}{3}$，$\frac{5\sqrt{3}}{3}$．
点评 本题考查的是正多边形和圆，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
相关题目