Question

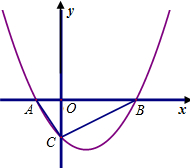
如图，抛物线y=ax²-2x+c经过直线y=x-3与坐标轴的两个交点A、B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．
（1）求此抛物线的解析式；
（2）⊙M是过A、B、C三点的圆，连接MC、MB、BC，求劣弧CB的长；（结果用精确值表示）
（3）点P为抛物线上的一个动点，求使S_△APC：S_△ACD=5：4的点P的坐标．（结果用精确值表示）

Answer 1

（1）把x=0和y=0分别代入y=x-3，
得当x=0时，y=-3；
当y=0时，x=3．
∴A（3，0），B（0，-3）．
把x=0时，y=-3；当y=0时，x=3代入y=ax²-2x+c，
得

c=-3 9a-6+c=0

，
解得：

c=-3 a=1

，
∴y=x²-2x-3．

（2）当y=0时，x²-2x-3=0，
解得x₁=3，x₂=-1．
∴C（-1，0）
∴AC=4，BC=

10

．
∵OA=OB=3，
∴∠CAB=45°，
∴∠CMB=90度．
∴MB=MC=

5

∴

BC

的长是

5

2

π．

（3）∵y=x²-2x-3的对称轴是x=-

b

2a

=1，
当x=1时，y=-4，
∴D（1，-4）．
∴S_△ACD=

1

2

×4×4=8，
∴S_△APC=10．
设存在点P（x，y），
∴|y|=5．
∴y=5时，x²-2x-3=5，
解得x₁=4，x₂=-2，
当y=-5时，P点不在抛物线上，
∴P₁（4，5），P₂（-2，5）．