题目内容
若x•xm•xn=x14，求m+n．
解：∵x•xm•xn=x1+m+n=x14，
∴1+m+n=14，
∴m+n=13．
分析：根据同底数幂的乘法法则进行计算即可．
点评：本题考查的是同底数幂的乘法，即底数不变，指数相加．
∴1+m+n=14，
∴m+n=13．
分析：根据同底数幂的乘法法则进行计算即可．
点评：本题考查的是同底数幂的乘法，即底数不变，指数相加．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，BC=1，AC=2，把边长分别为x1，x2，x3，…，xn的n个正方形依次放入△ABC中，请回答下列问题：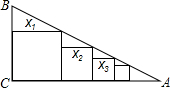
（1）按要求填表：
（2）第n个正方形的边长xn= ；
（3）若m，n，p，q是正整数，且xm•xn=xp•xq，试判断m，n，p，q的关系．
（1）按要求填表：
| n | 1 | 2 | 3 |
| xn |
（3）若m，n，p，q是正整数，且xm•xn=xp•xq，试判断m，n，p，q的关系．
如图，在Rt△ABC中，∠C=90°，BC=1，AC=2，把边长分别为x1，x2，x3，…，xn的n个正方形依次放入△ABC中，请回答下列问题：
（1）按要求填表：
（2）第n个正方形的边长xn=______；
（3）若m，n，p，q是正整数，且xm•xn=xp•xq，试判断m，n，p，q的关系．
（1）按要求填表：
| n | 1 | 2 | 3 |
| xn |
（3）若m，n，p，q是正整数，且xm•xn=xp•xq，试判断m，n，p，q的关系．