题目内容
已知:如图,AB、CD为⊙O的两条直径,M、N分别为AO、BO的中点.(1)求证:四边形CMDN为平行四边形;
(2)四边形CMDN能够是菱形吗?若能,你知道需要添加什么条件吗?

【答案】分析:(1)因为M、N分别为AO、BO的中点,所以AO=OB,因为OC=OD所以四边形CMDN为平行四边形
(2)根据菱形的判定方法,可添加两直径互相垂直时,四边形CMDN是菱形.
解答:(1)证明:∵AB是直径,OA=OB,M、N分别为AO、BO的中点,
∴OM= OA,ON=
OA,ON= OB,
OB,
∴OM=ON,
∵OC=OD,
∴四边形CMDN为平行四边形;
(2)解:添加条件:CD⊥AB.
∵CD⊥AB,点O是AB的中点,∴CD是AB的中垂线,∴CM=CN,
∴平行四边形CMDN是菱形
点评:本题利用了对角线互相平分的四边形是平行四边形和一组邻边相等的平行四边形是菱形的判定方法.还利用中垂线的性质:中垂线上的点到线段两个端点的距离相等.
(2)根据菱形的判定方法,可添加两直径互相垂直时,四边形CMDN是菱形.
解答:(1)证明:∵AB是直径,OA=OB,M、N分别为AO、BO的中点,
∴OM=
 OA,ON=
OA,ON= OB,
OB,∴OM=ON,
∵OC=OD,
∴四边形CMDN为平行四边形;
(2)解:添加条件:CD⊥AB.
∵CD⊥AB,点O是AB的中点,∴CD是AB的中垂线,∴CM=CN,
∴平行四边形CMDN是菱形
点评:本题利用了对角线互相平分的四边形是平行四边形和一组邻边相等的平行四边形是菱形的判定方法.还利用中垂线的性质:中垂线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.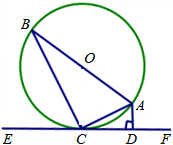 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.